Es waren im wesentlichen drei Ergebnisse experimenteller Forschung, die zur Entwicklung der
Quantentheorie geführt hatten: Schwarzkörperstrahlung, Atomsprektren und Radioaktivität.
Die Universalität des Kirchhoffschen Strahlungsgesetzes basierte auf den allgemeinen
Prinzipien der Thermodynamik. Eine Herleitung des speziellen gemessenen Strahlungsgesetzes
gelang Planck aber nur, indem er die Boltzmannsche Abzählmethode der statistischen Mechanik
für ununterscheidbare Teilchen abwandelte. Wie die Analyse der Energieschwankungen im
Strahlungsfeld zeigte, erwuchsen die Fluktuationen aus zwei Quellen: einer thermostatistischen
gemäß k T und einer quantenstatistischen gemäß ![]() . Die Existenz einer Nullpunktsenergie
für T = 0 sprengte den Rahmen der Thermodynamik. Neben der äußeren Wärmebewegung der
Atome mußten sie noch über innere Schwingungzustände verfügen, deren Energie nur für
. Die Existenz einer Nullpunktsenergie
für T = 0 sprengte den Rahmen der Thermodynamik. Neben der äußeren Wärmebewegung der
Atome mußten sie noch über innere Schwingungzustände verfügen, deren Energie nur für
![]() verschwände. Nach Einsteins Untersuchungen verteilte sich die Energie En dieser
Elementarresonatoren nur über ganzzahlige Vielfache n von
verschwände. Nach Einsteins Untersuchungen verteilte sich die Energie En dieser
Elementarresonatoren nur über ganzzahlige Vielfache n von ![]() :
:
![]()
Im Grundzustand für n = 0 blieb noch die Nullpunktsenergie. Einsteins Analyse der Absorption
und Emission von Lichtquanten durch die Elementarresonatoren im Strahlungsfeld führte zu der
Annahme spontaner Emission, ganz so wie beim radioaktiven Zerfall. Was war die Ursache dieser
Zufälligkeit, die den Dingen gleichsam innewohnte? Konnte es, wie bei der Brownschen Bewegung,
eine unterliegende Schicht der Ordnung geben, aus der die Spontanzerfälle durch Mittelung
verstanden werden konnten? Erforderte die Quantentheorie eine Erweiterung der statistischen
Mechanik?
Im Gegensatz zu Einstein, suchte Bohr nicht nach einer objektiven Ursache des Zufalls in den Mikrovorgängen. Im ging es eher um eine selbstkonsistente Theorie, die den Einfluß der Meßsituation zu berücksichtigen hatte. Seiner Komplementaritäts-Philosophie entsprechend, daß man nicht zugleich denken und über das Denken denken könne, dürfe man auch nicht versuchen, zugleich Teilchen- und Welleneigenschaften der Objekte messen zu wollen. So wie man den Bewußtseinsstrom störe, wenn man ihn reflektiere, verflüchtige sich auch die Interferrenz, wenn man die Bahnen der interferrierenden Quanten verfolge. Seine Komplementaritäts-Philosophie hatte ihm bei der Formulierung des Atommodells gute Dienste erwiesen. Die diskreten Strahlungsübergänge zwischen den Energieniveaus im Atom verband er geschickt mit der Annahme strahlungsloser Elektronenzustände, die als stehende Wellen gleichsam den Kern umhüllten. Die Quantisierung der Elektronenwelle erfolgt dann durch ganzzahlige Verteilung der jeweiligen Wellenlängen des Schwingungszustandes über den Atomumfang.
Aufgrund der endlichen Größe des Wirkungsquantums stört andererseits der mit jeder Messung verbundene Austausch von Energiequanten das Meßobjekt. Sind Messungen aber sogar am absoluten Nullpunkt nicht störungsfrei möglich, so werden die Ergebnisse mehrerer Messungen im allgemeinen nicht mehr unabhängig voneinander sein können und von der Reihenfolge abhängen. Ein solcher Einfluß der meßpraktischen Operationen konnte in der Theorie durch mathematische Operatoren berücksichtigt werden, die im allgemeinen nicht vertauschten.
Im Anschluß an die Poisson-Klammern der Hamiltonschen Mechanik gelang
Heisenberg 1926 die Formulierung einer algebraischen Theorie, in der er die Meßoperatoren durch
Matrizen darstellte. Er ging aus von den kanonisch-konjugierten Variablen des Phasenraumes
p und q, für die er aber eine nichtverschwindende Vertauschungsrelation annahm:
![]() . Nach Heisenberg wird also mit dem Wirkungsquantum eine nichtkommutative
Algebra der Atome eingeführt. Im Kontinuumsübergang großer Quantenzahlen konnte die
Matrizenmechanik
mit
. Nach Heisenberg wird also mit dem Wirkungsquantum eine nichtkommutative
Algebra der Atome eingeführt. Im Kontinuumsübergang großer Quantenzahlen konnte die
Matrizenmechanik
mit ![]() auf die Hamiltonschen Mechanik zurückgeführt werden.
Die Anwendung seiner Matrizenmechanik auf beliebige Hamiltonsche Systeme, ergab eine dynamische
Grundgleichung für den Meßoperator A in Abhängigkeit von der Zeit und dem Energieoperator H:
auf die Hamiltonschen Mechanik zurückgeführt werden.
Die Anwendung seiner Matrizenmechanik auf beliebige Hamiltonsche Systeme, ergab eine dynamische
Grundgleichung für den Meßoperator A in Abhängigkeit von der Zeit und dem Energieoperator H:
![]()
Die algebraische Berechnung der möglichen Energieniveaus nk für den Energieoperator des Elementarresonators n lieferte auch den Grundzustand der Nullpunktsenergie, den die kommutative Theorie für kontinuierliche Energieverteilungen nicht voraussagte:
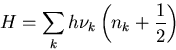
Bohr und Heisenberg waren derart beeindruckt von ihrer neuen Theorie, daß sie einen fundamentalen Bruch mit dem mechanistischen Weltbild annahmen und fortan die sogenannte Quantenmechanik als moderne Physik von der klassischen Physik des 19. Jahrhunderts abzugrenzen suchten. Aus den Vertauschungsrelationen konnte Heisenberg seine berühmt gewordenen Unbestimmtheitsrelationen für kanonisch-konjugierte Variablen ableiten, die in der klassischen Theorie keine Entsprechung hatten. Danach war es z.B. unmöglich, Impuls und Ort eines Elektrons zugleich beliebig genau zu messen. Heisenberg sah in der Quantenmechanik den schon von Einstein in der speziellen Relativitätstheorie fruchtbar gemachten Positivismus Machs weitergeführt. In seiner grundlegenden Arbeit Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik ging es ihm darum, den Kampf der Meinungen um Diskontinuums- und Kontinuumstheorie, Korpuskeln und Wellen durch Beziehungen zwischen experimentell gegebenen Zahlen zu ersetzen. Heisenberg glaubte, die Entstehung der klassischen ,,Bahn`` so formulieren zu können: Die ,,Bahn`` entsteht erst dadurch, daß wir sie beobachten.
Was mag Heisenberg zu einem derartigen Schritt in den Subjektivismus, gleichsam von der Seins- in die Erkenntistheorie, bewogen haben? Einstein hatte mit der allgemeinen Relativitätstheorie seinen Positivismus der frühen Phase überwunden. In seiner Feldgleichung hatte er einen objektiven Zusammenhang zwischen Materieverteilung und Raumzeit gefunden. Mit dem Erfolg seiner Gravitationstheorie verknüpfte er seinen Maßstab der Vollkommenheit: Es ist klar, daß man im allgemeinen eine Theorie als umso vollkommener beurteilen wird, eine je einfachere Struktur sie zugrunde legt und je weiter die Gruppe ist, bezüglich welcher die Feldgleichungen invariant sind.
Diesem Ideal fühlte sich auch Schrödinger verbunden, als er im Anschluß an die Hamiltonsche Wirkungswelle ebenfalls 1926 seine Wellengleichung der Materie formulierte:
![]()
Im Gegensatz zur Heisenbergschen Matritzengleichung für Meßoperatoren, fand die Schrödingergleichung
unter den Physikern rasche Aufnahme, da sie in gewohnter Weise mit einer Differentialgleichung
arbeiten konnten. Für Heisenberg mag das ein Grund gewesen sein, sich über den anschaulichen
Inhalt seiner Theorie Gedanken zu machen. Born
benutzte die Schrödingergleichung
1927 in der Streutheorie zur Berechnung von Wirkungsquerschnitten für Streuexperimente mit
Teilchenbeschleunigern. In diesem Zusammenhang gelang es ihm, die Wellenfunktion ![]() als
Wahrscheinlichkeitsamplitude zu deuten. D.h. ihr Betragsquadrat
als
Wahrscheinlichkeitsamplitude zu deuten. D.h. ihr Betragsquadrat ![]() sah er
als Wahrscheinlichkeitsdichte an, so daß
sah er
als Wahrscheinlichkeitsdichte an, so daß ![]() das Wahrscheinlichkeitsmaß
darstellte, einen Zustand im Intervall dq des hochdimensionalen Konfigurationsraums zu finden.
Da Schrödinger kurze Zeit später die Äquivalenz zwischen der Wellen- und Matrizenmechanik
beweisen konnte, drohte die Heisenbergsche Theorie ins Hintertreffen zu geraten. Zumal de'Broglie 1927 auf
die Ergänzung der Schrödingergleichung durch eine Potentialgleichung hingewiesen hatte, nach der
die Teilchenbahnen in gewohnter Weise aus einem Potential berechnet werden konnten. Die Interpretation
dieses Quantenpotentials fiel allerdings der vehementen Kritik Paulis zum Opfer, da es eine
instantane Wirkungsausbreitung zur Folge hatte, die der Relativitätstheorie widersprach. Für eine
Wahrscheinlichkeitswelle mochte das noch angehen, aber für eine Wirkungswelle? Einsteins Haltung
blieb zwiespältig. Die Wellenfunktion hielt er für ein Gespensterfeld und am instantanen
Quantenpotential störte ihn natürlich die fehlende relativistische Invarianz. De'Broglie
deutete die Wellenfunktion in seiner Vervollständigung der Quantenmechanik als Führungswelle,
die den Teilchen gleichsam den Weg wies, ganz so wie ein Kraftfeld die Bahnen der Massen oder
Ladungen bestimmte. Im Gegensatz zur Gravitation oder zum Elektromagnetismus Einsteins,
war die Wirkung der Führungswelle auf die Teilchen jedoch einseitig und instantan.
das Wahrscheinlichkeitsmaß
darstellte, einen Zustand im Intervall dq des hochdimensionalen Konfigurationsraums zu finden.
Da Schrödinger kurze Zeit später die Äquivalenz zwischen der Wellen- und Matrizenmechanik
beweisen konnte, drohte die Heisenbergsche Theorie ins Hintertreffen zu geraten. Zumal de'Broglie 1927 auf
die Ergänzung der Schrödingergleichung durch eine Potentialgleichung hingewiesen hatte, nach der
die Teilchenbahnen in gewohnter Weise aus einem Potential berechnet werden konnten. Die Interpretation
dieses Quantenpotentials fiel allerdings der vehementen Kritik Paulis zum Opfer, da es eine
instantane Wirkungsausbreitung zur Folge hatte, die der Relativitätstheorie widersprach. Für eine
Wahrscheinlichkeitswelle mochte das noch angehen, aber für eine Wirkungswelle? Einsteins Haltung
blieb zwiespältig. Die Wellenfunktion hielt er für ein Gespensterfeld und am instantanen
Quantenpotential störte ihn natürlich die fehlende relativistische Invarianz. De'Broglie
deutete die Wellenfunktion in seiner Vervollständigung der Quantenmechanik als Führungswelle,
die den Teilchen gleichsam den Weg wies, ganz so wie ein Kraftfeld die Bahnen der Massen oder
Ladungen bestimmte. Im Gegensatz zur Gravitation oder zum Elektromagnetismus Einsteins,
war die Wirkung der Führungswelle auf die Teilchen jedoch einseitig und instantan.
Die sich unter der Vorherrschaft Bohrs schnell verbreitende Kopenhagener Deutung der Quantenmechanik machte aus der Not, es mit einem Gespensterfeld zu tun zu haben, die Tugend, daß es sich dabei lediglich um das Wissen handelte, das wir von einem atomaren System haben könnten. Dieses Wissen mußte darüber hinaus die gesamte physikalische Situation des Experiments umfassen und garantierte insofern Vollständigkeit. Die Ergänzung der Wissensfunktion als Lösung der Schrödingergleichung durch Teilchenbahnen als Wirkung eines Quantenpotentials wurde damit überflüssig. Der Mathematiker von Neumann brachte die Quantenmechanik 1932 in eine mathematische Form, die bis heute Bestand hat und von den Abweichlern gerne als orthodox bezeichnet wird. Die atomaren Zustände werden darin als Vektoren in einem hochdimensionalen, komplexen Zustandsraum, dem Hilbertraum, dargestellt. Die Meßoperatoren werden zu selbstadjungierten Operatoren, die auf die Zustandsvektoren anzuwenden sind, deren Dynamik durch unitäre Transformationen beschrieben wird. Als Wahrscheinlichkeitsmaß fungiert die Summe der Betragsquadrate der Eigenwerte bei der Entwicklung der Zustandsvektoren nach dem vollständigen System von Eigenfunktionen der Meßoperatoren. Einem Theorem Gleasons zufolge ist ein solches Wahrscheinlichkeitsmaß sogar das einzig mögliche im Hilbertraum.
Von Neumann verfolgte mit seiner mathematisch rigorosen Formulierung der
Quantenmechanik aber noch ein weiteres Ziel. Er wollte die Möglichkeit einer Ergänzung
seiner Darstellung durch verborgene Variablen ausschließen. Dazu konnte er innerhalb
seines Formalismus einen strengen mathematischen Beweis führen. Sein Beweis enthielt jedoch
eine wesentliche, physikalisch unsinnige, Voraussetzung und wurde von den Physikern, die
sich die Mühe machten, ihn nachzuvollziehen, nicht ernst genommen. Das waren zunächst aber
nur sehr wenige. Die Mehrheit begnügte sich mit dem Glauben, daß die Bohr-Heisenbergsche
Quantenmechanik nunmehr sogar durch einen berühmten Mathematiker als nicht durch verborgene
Variablen erweiterbar bewiesen worden war. De`Broglies Theorie wurde vergessen, er selbst
konvertierte zur Orthodoxie. 1935 allerdings trat Einstein wieder auf den Plan und fragte
in einer Gemeinschaftsarbeit mit Podolsky und Rosen: Can quantum mechanical description
of physical reality be considered complete? In einem Gedankenexperiment mit korrelierten
Quantenzuständen wiesen die Autoren nach, daß die Quantenmechanick nicht vollständig
sein könne, wenn sie realistisch und lokal sein solle. Der Orthodoxie gelang eine
Rettung der Vollständigkeit natürlich durch die Kritik des klassischen Realitätspostulats.
Die de`Brogliesche Erweiterung durch ein nichtlokales Quantenpotential war andererseits mit
der Einsteinschen Realitätsauffassung vereinbar. Einstein hatte sein Dilemma mal wieder
in brillianter Klarheit auf den Punkt gebracht. Da er Realismus und Lokalität für unabdingbar
hielt, stand die Quantenmechanik für ihn weiterhin in dem Ruch, unvollständig zu sein.
Die Avantgarde der Theoretiker nahm allerdings kaum Notiz von der Einsteinschen Arbeit.
Die jungen Physiker waren vollends damit beschäftigt, eine relativistisch invariante
Quantentheorie durch Quantisierung des Materiefeldes und des elektromagnetischen Feldes
auf den Weg zu bringen, die später Quantenelektrodynamik (QED) genannt wurde.
Sie begannen damit, die unverstandenen Meßergebnisse beim Experimentieren
mit Atomen in elektromagnetischen Feldern zu erklären. Die Experimente legten für das
magnetische Moment ![]() des Elektrons folgenden Ausdruck nahe:
des Elektrons folgenden Ausdruck nahe:
![]()
Der g-Faktor des gyromagnetischen Verhältnisses lag bei 2 und der Ausdruck ![]() stand
für den Eigendrehimpuls (Spin) des Elektrons. Pauli erweiterte die Schrödingergleichung
für Elektronen im elektromagnetischen Feld um einen Term, der die Wechselwirkung zwischen
Elektronenspin
stand
für den Eigendrehimpuls (Spin) des Elektrons. Pauli erweiterte die Schrödingergleichung
für Elektronen im elektromagnetischen Feld um einen Term, der die Wechselwirkung zwischen
Elektronenspin ![]() und Magnetfeld
und Magnetfeld ![]() beschrieb:
beschrieb:
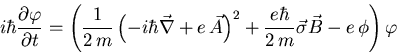
![]() meint das Dreier-Vektorpotential und
meint das Dreier-Vektorpotential und ![]() steht für das elektrostatische
Skalarpotential. Unter Berücksichtigung des Ausschließungsprinzips für die
unterscheidbaren Elektronen mit halbzahligem Spin stimmte die Pauligleichung gut mit
den Experimentierergebnissen überein. Einen Theoretiker ließ sie allerdings unbefriedigt,
da sie nicht aus ersten Prinzipien folgte.
steht für das elektrostatische
Skalarpotential. Unter Berücksichtigung des Ausschließungsprinzips für die
unterscheidbaren Elektronen mit halbzahligem Spin stimmte die Pauligleichung gut mit
den Experimentierergebnissen überein. Einen Theoretiker ließ sie allerdings unbefriedigt,
da sie nicht aus ersten Prinzipien folgte.
Warum gab es einen Zusammenhang zwischen Spin und Statistik? Planck hatte bereits 1900 eine Abzählmethode für ununterscheidbare Elementarresonatoren annehmen müssen. Die von Einstein daraufhin postulierten Lichtquanten hatten die ganzzahlige Spinquantenzahl eins. Im Anschluß an Arbeiten Boses und Fermis um die Mitte der 1920er Jahre gab es einen generellen Zusammenhang zwischen der thermischen Verteilung der mittleren Besetzungszahlen <ni> für Quantenzustände gleichartiger bzw. ungleichartiger Teilchen. Die Verteilungsfunktionen nach Bose <ni>B und Fermi <ni>F unterschieden sich durch das Vorzeichen im Nenner:
![]()
Die Plancksche Abzählmethode für Teilchen mit ganzzahligen Spinquantenzahlen hat eine symmetrische Wellenfunktion zur Folge und korrespondiert mit der Bosestatistik <ni>B. Das Paulische Ausschließungsprinzip für Teilchen mit halbzahligen Spinquantenzahlen führt auf eine antisymmetrische Wellenfunktion, der eine Fermistatistik <ni>F entspricht. Die von Einstein erstmals postulierten Feldquanten des elektromagnetischen Feldes zählen zu den Bosonen. Die Feldquanten der Materiewellen dagegen verhalten sich wie Fermionen.
Warum haben die fundamentalen Bausteine der Materie, die Fermionen, halbzahligen Spin?
Für Dirac lag die Antwort auf diese Frage in der Forderung, daß die Wahrscheinlichkeit
immer positiv sein müsse bzw. : ![]() . Und warum gibt es überhaupt
Bosonen und Fermionen? Weinberg stellte dazu folgende Plausibilitätsbetrachtung an:
First note that if two particles with momenta and spins
. Und warum gibt es überhaupt
Bosonen und Fermionen? Weinberg stellte dazu folgende Plausibilitätsbetrachtung an:
First note that if two particles with momenta and spins ![]() belong to
identical species n, then the state-vector
belong to
identical species n, then the state-vector
![]() and
and
![]() represent the same physical state;
if this were not the case then the particles would be distinguished by their order in the
labelling of the state-vector, and the first listed would not be identical with the second.
Since the two state-vectors are physically indistinguishable, they must belong to the same ray,
and so
represent the same physical state;
if this were not the case then the particles would be distinguished by their order in the
labelling of the state-vector, and the first listed would not be identical with the second.
Since the two state-vectors are physically indistinguishable, they must belong to the same ray,
and so
![]()
where ![]() is a complex number of unit value. We may regard this as part of the
definition of what we mean by identical particles. The crux of the matter is to decide on
what the phase factor may depend. If it depends only on the species index n, then we
are nerly done. Interchanging the two particles again, we find
is a complex number of unit value. We may regard this as part of the
definition of what we mean by identical particles. The crux of the matter is to decide on
what the phase factor may depend. If it depends only on the species index n, then we
are nerly done. Interchanging the two particles again, we find
![]()
![]()
Einstein hatte 1905 zwei fundamentale physikalische Prinzipien eingeführt: das
Quantisierungs- und das Geometrisierungsprinzip. Plancks Entdeckung der Proportionalität
von Energie und Frequenz für die sich im Strahlungsgleichgewicht
befindlichen Elementarresonatoren des Hohlraums deutete er in kühner Weise als
Quantisierungsvorschrift und postulierte die Existenz diskreter Lichtquanten.
Und Lorentzens Kontraktionsgleichung für schnell bewegte Körper gegenüber dem Äther
reformulierte er als Relativitätsprinzip
,
dem alle physikalischen Theorien zu genügen hätten.
Das Quantisierungsprinzip hatte zur Entdeckung zweier fundamentaler Teilchenarten
geführt, den Bosonen und den Fermionen. Zu den Bosonen zählten die als
Quanten des elektromagnetischen Feldes postulierten Lichtquanten, die später auch
Photonen genannt wurden. Ihre Wellengleichung war seit Maxwells Herleitung von 1864
bekannt. Als Vertreter der Fermionen wurde das Elektron erkannt, das erstmals 1858
in den Kathodenstrahlen experimentell in Erscheinung trat. Schrödinger hatte die
erste Wellengleichung
für Elektronen
im elektrostatischen Potential des Protons formuliert. Nach der Quantisierung der
kanonisch-konjugierten Variablen des Phasenraumes durch Einführung des Energieoperators
H als Funktion des Orts- und Impulsoperators, stand noch die Quantisierung der Felder
aus. Ihre Durchführung zur Erlangung der entsprechenden Feldoperatoren gelang Heisenberg
und Pauli 1929. Ihre Untersuchungen markieren den Beginn der Quantenfeldtheorien (QFT).
Die Übertragung des Relativitätsprinzips der Elektrodynamik auf die
Gravitationstheorie führte in der allgemeinen Relativitätstheorie (ART) zum
Geometrisierungsprinzip. Aus den konstanten Koeffizienten ![]() der
Minkowski-Metrik in flacher Raumzeit wurden die kontinuierlich veränderbaren Metrik-Koeffizienten
der
Minkowski-Metrik in flacher Raumzeit wurden die kontinuierlich veränderbaren Metrik-Koeffizienten
![]() , deren Änderung ein affiner Zusammenhang
, deren Änderung ein affiner Zusammenhang ![]() bestimmte, der auch
Verschiebungs- oder Führungsfeld genannt wurde. Nach dem Äquivalenzprinzip läßt sich
ein konstantes Gravitationsfeld durch ein gleichförmig beschleunigtes Bezugssystem
nachbilden. Für die Geodätengleichung in gekrümmter
Riemannscher Raumzeit ergab das mit der Eigenzeit
bestimmte, der auch
Verschiebungs- oder Führungsfeld genannt wurde. Nach dem Äquivalenzprinzip läßt sich
ein konstantes Gravitationsfeld durch ein gleichförmig beschleunigtes Bezugssystem
nachbilden. Für die Geodätengleichung in gekrümmter
Riemannscher Raumzeit ergab das mit der Eigenzeit ![]() gemäß
gemäß
![]() für die frei fallenden
Koordinatensysteme
für die frei fallenden
Koordinatensysteme ![]() folgenden Zusammenhang:
folgenden Zusammenhang:
![]()
Dabei stellte sich natürlich sofort die Frage, ob die flache Metrik ![]() bloß in krummlinigen Koordinaten geschrieben worden war oder durch die Gravitation zu
bloß in krummlinigen Koordinaten geschrieben worden war oder durch die Gravitation zu
![]() gekrümmt wurde:
gekrümmt wurde:
![]()
Der Metrik kam jedenfalls eine Doppelbedeutung zu: als metrischer Tensor der vierdimensionalen
Riemannschen Raumzeit und zur Repräsentation des Gravitationsfeldes. Existierte die Raumzeit
überhaupt noch unabhängig von der Gravitation?
Ein nichtverschwindender Krümmungstensor R drückte die Existenz eines Gravitationsfeldes aus:
![]() . Für Einstein bildeten die
physikalischen Felder die Basis der Raumzeitgeometrie. Nach ihm dynamisierte das Gravitationsfeld
die Geometrie der Raumzeit. Den Zusammenhang zwischen Krümmungstensor R und Energie-Impulstensor
T mit der Gravitationskonstanten G lieferte 1915 Einsteins berühmte Feldgleichung:
. Für Einstein bildeten die
physikalischen Felder die Basis der Raumzeitgeometrie. Nach ihm dynamisierte das Gravitationsfeld
die Geometrie der Raumzeit. Den Zusammenhang zwischen Krümmungstensor R und Energie-Impulstensor
T mit der Gravitationskonstanten G lieferte 1915 Einsteins berühmte Feldgleichung:
![]()
D.h. die gesamte Energie aller Wechselwirkungen trägt zur Krümmung der Raumzeit bei.
Eine Quantentheorie der Gravitation ist allerdings bis heute nicht gelungen.
Die masselosen Spin-2-Gravitonen werden lediglich in linearer Näherung durch
Quantisierung der Gravitationswellen gewonnen. Die Annahme kontinuierlicher
Teilchenbahnen im gekrümmten Raum widerspricht zwar der Kopenhagener Deutung,
steht aber im Einklang mit den Teilchenbahnen unter dem Einfluß der
de'Broglieschen Führungswelle.
Ein weiteres Fundamentalprinzip zur Geometrisierung der Physik wurde 1918 von dem
Mathematiker Weyl eingeführt. Bei seinem Versuch,
Gravitation und Elektromagnetismus zu vereinheitlichen, erweiterte er
das Prinzip der lokalen Bewegungsinvarianz der ART durch die Forderung nach lokaler
Skaleninvarianz der Maßstäbe, die er Eichinvarianz nannte. Das Verschiebungsfeld
![]() ergänzte er dafür um einen Ausdruck, der neben den Metrik-Koeffizienten zudem
die Komponenten eines Vektorpotentials enthielt, das in üblicher Weise die Berechnung
des Feldtensors erlaubte. Die physikalischen Konsequenzen dieser Erweiterung der ART
hielten allerdings nicht der Kritik Einsteins stand. Nachdem Weyl aber 1929 die
Eichinvarianz auf die Quantentheorie übertragen hatte, wurde den Physikern die ganze
Tragweite seines Konzeptes bewußt und sie machten es zu einem der leitenden Prinzipien
bei der Formulierung der QFT der subatomaren Wechselwirkungen.
ergänzte er dafür um einen Ausdruck, der neben den Metrik-Koeffizienten zudem
die Komponenten eines Vektorpotentials enthielt, das in üblicher Weise die Berechnung
des Feldtensors erlaubte. Die physikalischen Konsequenzen dieser Erweiterung der ART
hielten allerdings nicht der Kritik Einsteins stand. Nachdem Weyl aber 1929 die
Eichinvarianz auf die Quantentheorie übertragen hatte, wurde den Physikern die ganze
Tragweite seines Konzeptes bewußt und sie machten es zu einem der leitenden Prinzipien
bei der Formulierung der QFT der subatomaren Wechselwirkungen.
Dirac verallgemeinerte 1927 die Schrödingergleichung für Elektronen im elektromagnetischen
Feld zu einer relativistisch-invarianten Wellengleichung der Materie. Für ein freies
Elektron machte er folgenden Ansatz: ![]() .
Mit
.
Mit ![]() und
und ![]() erhielt er folgende Gleichung für Vierervektoren x und Vierermatrizen
erhielt er folgende Gleichung für Vierervektoren x und Vierermatrizen ![]() im
elektromagnetischen Feld des Vierervektorpotentials
im
elektromagnetischen Feld des Vierervektorpotentials ![]() :
:
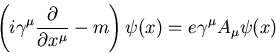
Diracs Gleichung erklärte zwar die Feinstrukturen im Wasserstoffatom sowie den Elektronenspin und
den g-Faktor im magnetischen Moment. Da der Magnetismus allgemein als relativistischer Effekt
verstanden werden kann, war das zu erwarten gewesen. Zudem folgt die Diracgleichung auch schlicht
aus der Multiplikation der quellenfreien Maxwellgleichung mit dem Paulivektor der Spinmatrizen.
Das bemerkte aber erst Sallhofer 1978.
Als schwerwiegender erwies sich das Problem negativer Energien. Dirac hatte sich nämlich mit Lösungen
für negative Energien herumzuschlagen gemäß ![]() . Als Ausweg postulierte
er die Existenz einer Art von Antiteilchen, die er als Lochzustände im
Vakuum ansah. Als Anderson 1932 das Positron entdeckte, konnte es als Lösung der Diracgleichung
verstanden werden. Feynman faßte den Triumpf Diracs in seiner Memorial Lecture zusammen:
If we insist that particles can only have positive energies, then you cannot avoid
propagation outside the light cone. If we look at such propagation from a different frame,
the particle is traveling backwards in time: it is an antiparticle. Then, looking at the idea
that the total probability of something happening must be one, we saw that the extradiagrams
arising because of the existence of antiparticles and pair production implied Bose statistics
for spinless particles. When we tried the same idea on fermions, we saw that exchanging particles
give us a minus sign: they obey Fermi statistics. The general rule was that a double time
reversal is the same as a 360o rotation. This gave us the connection between spin and
statistics and the Pauli exclusion principle for spin 1/2.
. Als Ausweg postulierte
er die Existenz einer Art von Antiteilchen, die er als Lochzustände im
Vakuum ansah. Als Anderson 1932 das Positron entdeckte, konnte es als Lösung der Diracgleichung
verstanden werden. Feynman faßte den Triumpf Diracs in seiner Memorial Lecture zusammen:
If we insist that particles can only have positive energies, then you cannot avoid
propagation outside the light cone. If we look at such propagation from a different frame,
the particle is traveling backwards in time: it is an antiparticle. Then, looking at the idea
that the total probability of something happening must be one, we saw that the extradiagrams
arising because of the existence of antiparticles and pair production implied Bose statistics
for spinless particles. When we tried the same idea on fermions, we saw that exchanging particles
give us a minus sign: they obey Fermi statistics. The general rule was that a double time
reversal is the same as a 360o rotation. This gave us the connection between spin and
statistics and the Pauli exclusion principle for spin 1/2.
Im Anschluß an die Arbeiten Diracs, Heisenbergs und Paulis entwickelten in den 1940er Jahren
Feynman, Schwinger und Tomonaga
die Eichtheorie der elektromagnetischen Wechselwirkung. Die weiteren
Eichtheorien
des
Standard-Modells zur Beschreibung der starken und schwachen Wechselwirkung im Bereich der
subatomaren Physik wurden in den 1960er und 70er Jahren von Gell-Mann
,
Glashow, Salam und Weinberg
sowie
't Hooft und Veltman
entwickelt und folgten im Prinzip dem gleichen Schema. In ihm werden die Bauteilchen oder
Fermionen (Quarks, Leptonen) durch Materiefelder beschrieben. Die Existenz der Austauschteilchen
oder Bosonen (Gluonen, W/Z-Bosonen, Photon, Graviton) folgt mathematisch aus der Forderung,
daß die Materiefelder eichinvariant sein sollen und die Austauschströme dem Äquivalenzprinzip
zu genügen haben.
Bei der Vereinheitlichung der elektromagnetischen mit der schwachen und starken Wechselwirkung
der Kernkräfte kam allerdings die Schwierigkeit hinzu, daß die Austauschteilchen oder
Eichbosonen der schwachen Wechselwirkung, die W/Z-Bosonen, kurzreichweitig wirken und
damit im Gegensatz zu den Photonen eine Ruhemasse haben. Um die Konsistenz der
vereinheitlichten elektroschwachen Theorie zu erhalten, wurde ein Mechanismus übernommen, der
schon seit langem in der Festkörperphysik benutzt und von Higgs auf die Hochenergiephysik
übertragen worden war. Danach können die Eichbosonen ihre Masse aus dem Symmetriebruch
eines angenommenen Vakuumfeldes erhalten. So wie im Kristallgitter eines Festkörpers
z.B. die Cooperpaare beim Übergang zur Supraleitung auskondensieren, bilden sich im
Phasenübergang des Vakuums die Massen der Eichbosonen. D.h. vor dem Symmetriebruch
bei hohen Energien sind die Austauschteilchen masselos und unbegrenzt weit wirksam. Nach
dem Symmetriebruch bzw. Phasenübergang erlangen die W/Z-Bosonen mit abnehmender Energie
ihre Masse, wirken nur noch über kurze Distanzen und entkoppeln von dem Photonenfeld
der QED. Neben dem elektromagnetischen ZPF ist das Vakuum mit dem Higgsfeld um eine weitere
Struktur bereichert worden. Nach dem Higgsboson als Austauschteilchen zwischen
elektroschwachem und Vakuumfeld wird seit Jahren intensiv gefahndet. Da seine Masse aber
bei über ![]() vermutet wird, dürfte es erst mit der nächsten Beschleunigergeneration
nachweisbar sein.
vermutet wird, dürfte es erst mit der nächsten Beschleunigergeneration
nachweisbar sein.
Das prinzipielle Vorgehen bei der Formulierung einer Eichtheorie soll am Beispiel der QED näher erläutert werden. Der Clou dabei ist, daß die Forderung nach lokaler Eichinvarianz des Materiefeldes die Existenz eines Eichfeldes zur Folge hat, das die Wechselwirkung vermittelt. In der QED wird das freie Materiefeld der Elektronen durch die Diracgleichung beschrieben, die folgender Lagrangefunktion LD entspricht:
![]()
Als globale Eichinvarianz wird die Unabhängigkeit der Lagrangefunktion von einer
globalen Änderung der Wellenphase bezeichnet. D.h. ![]() läßt
LD unverändert und hat Ladungserhaltung zur Folge. Denn aus dem ersten Noetherschen
Theorem folgt die Existenz eines Stromes, für den die Kontinuumsgleichung gilt:
läßt
LD unverändert und hat Ladungserhaltung zur Folge. Denn aus dem ersten Noetherschen
Theorem folgt die Existenz eines Stromes, für den die Kontinuumsgleichung gilt:
![]() , wobei
, wobei ![]() .
.
Die weitergehende Forderung nach lokaler Eichinvarianz ![]() zieht die Existenz eines Eichpotentials nach sich:
zieht die Existenz eines Eichpotentials nach sich: ![]() .
Die Potentialkrümmung bzw. Rotation ergibt die Eichfeldstärke:
.
Die Potentialkrümmung bzw. Rotation ergibt die Eichfeldstärke:
![]() . Noetherstrom und Eichpotential
bestimmen den Wechselwirkungsterm:
. Noetherstrom und Eichpotential
bestimmen den Wechselwirkungsterm:
![]()
![]()
![]()
LQED = LD + LW + LM
Einstein hatte die Newtonsche Gravitationstheorie durch Geometrisierung zur ART verallgemeinert. Im Rahmen des eichtheoretischen Programms Weyls entspricht die lokale Eichinvarianz dem allgemeinen Relativitätsprinzip, nach dem die Gravitation unabhängig von der Wahl der Raumzeit-Koordinaten bzw. invariant bzgl. beliebiger kontinuierlicher Raumzeit-Transformationen sein sollte. Der Diracgleichung des Materiefeldes entspricht in der ART die Geodätengleichung in gekrümmter Raumzeit. Dem Ladungsstrom der QED korrespondiert der Energiestrom der ART. Und dem elektromagnetischen Feldtensor als Eichfeld entspricht das Verschiebungsfeld. Das Eichpotential korrespondiert mit dem metrischen Tensor und die Maxwellsche Feldgleichung steht der Einsteinschen Feldgleichung gegenüber. Im Wechselwirkungsbild der Eichtheorien wird das Gravitationsfeld als Wechselwirkungsfeld eines masselosen Spin-2-Bosons, des Gravitons, angenährt. Die lokale Lorentz-Invarianz der Gravitationstheorie einer Kopplung zwischen Graviton und Energie-Impulstensor hat nach Weinberg das Äquivalenzprinzip zwischen träger und schwerer Masse zur Folge: It seems to be impossible to construct any Lorentz-invariant quantum theory of particles of mass zero and spin two unless the corresponding classical field theory obeys the Principle of Equivalence
Im Rahmen der mathematischen Theorie der Faserbündel konnten die physikalischen Theorien der vier fundamentalen Wechselwirkungen gemäß NVP formal zusammengeführt werden. Ein physikalisches Verständnis des Zusammenhangs zwischen Teilchenphysik und Gravitationstheorie ist aber erst unter der Annahme einer weiteren Invarianzforderung möglich: der Supersymmetrie zwischen Bosonen und Fermionen. Die experimentelle Überprüfung der Niederenergieabschätzungen in der vereinheitlichten supersymmetrischen Theorie (SUSY) ebenso wie in der Theorie der Superstrings wird aber erst der nächsten Beschleunigergeneration am CERN oder bei DESY möglich sein.