Klassische Physik

Das Paradigma der klassischen Physik begann mit Galilei und wurde zum Vorbild für Wissenschaft schlechthin. Seit Galileis genialer Verbindung von mathematischer Argumentation und experimenteller Technik hat sich das Programm einer näherungsweise-vereinheitlichenden Behandlung der Naturbeobachtungen und Experimentierresultate im Zuge der Verwissenschaftlichung unserer Zivilisation zu einem Weltbild von faszinierender Reichhaltigkeit entwickelt. Die Extrapolationen des physikalischen Standardmodells erstrecken sich über 61 Größenordnungen und die Meßergebnisse sind mit einer Präzision von bis zu 14 Stellen mit den Folgerungen der Theorie vergleichbar. Die Quantentheorie lieferte neben der Relativitätstheorie nicht nur die Grundlage für das Standardmodell, sondern machte darüber hinaus auch Chemie und Biologie zu physikalischen Wissenschaften. Gegenwärtig dehnen die Physiker ihr Betätigungsfeld auf die Sozialforschung und die Wirtschaftswissenschaften aus. Das Programm einer sozialen Physik entstand bereits im Zuge der Aufklärung und wurde mit den verbessertern wissenschaflichen Methoden verfeinert. So nimmt es nicht wunder, daß die Behandlung stochastischer Prozesse bereits 1900 durch den Mathematiker Bachelier in die Ökonomie eingeführt wurde, fünf Jahre vor Einsteins grundlegender Arbeit zur Brownschen Bewegung.

Im Rahmen des näherungsweise-vereinheitlichenden Paradigmas (NVP) der neuzeitlichen Naturphilosophie führte Newton in seiner Gravitationstheorie die Galileischen Wurfparabeln und die Keplerschen Ellipsenbahnen auf ein gemeinsames Kraftgesetz zurück. Damit vereinigte er die Bewegungen von Kanonenkugeln auf der Erde mit den Planetenbahnen am Himmel. Zielgerichtete Geschoßbahnen im Schwerefeld der Erde wurden in gleicher Weise behandelt wie bewirkte Planetenbahnen im Gravitationsfeld der Sonne. Voltaire überhöhte die Newtonsche Mechanik zum mechanistischen Weltbild: Entweder ergibt sich alles aus dem notwendigen Wesen der Dinge oder aus der ewigen Ordnung, die ein absoluter Geist gestiftet hat. Wirk- und Zielursache wurden durch Euler und Lagrange im Prinzip der kleinsten Wirkung vereint:

$$\delta S = \delta \int L(q_i, \dot{q_i}, t) \, dt = 0.$$

Als Wirkung S wird das Produkt aus Energie und Zeit bezeichnet. Dem Integralprinzip der Wirkungsvariation $\delta S$ entspricht das Differentialprinzip der Bewegungsgleichung:

$${d \over dt} {\partial L \over {\partial \dot{q_i}}} - {\partial L \over {\partial {q_i}}} = 0.$$

Die Lagrangefunktion L wird aus der Differenz von Bewegungs- und potentieller Energie bestimmt: L = T - V.

Neben der Bewegung von Gestirnen am Himmel und Geschossen auf der Erde, haben sich die Menschen von altersher auch für die Ausbreitung von Lichtstrahlen und Wasserwellen interessiert. In der Eulerschen Mechanik der Kontinua wurden nicht mehr diskrete Massenpunkte m_i betrachtet, sondern im Grenzübergang dm kontinuierliche Massendichten $\rho = dm/dv$ per Volumenelement dv berechnet. Die kontinuierliche Ausbreitung periodischer Schwingungen in einem Medium wurde in linearer Näherung durch Wellengleichungen beschrieben:

$${1 \over c^2} {{{\partial}^2 \rho} \over {\partial t^2}} = \triangle \rho (\vec{r}, t)$$

In der Wellengleichung steht $\triangle$ für den Laplace-Operator, $\vec{r}$ bezeichnet den Ortsvektor und c bedeutet die Wellengeschwindigkeit. Akustik und Optik wurden zu Teilgebieten der Mechanik. Die Lösungen der Wellengleichung lieferten nicht nur ein Verständnis der Schallausbreitung in Gasen, Flüssigkeiten und Festkörpern, sondern auch die Berechnung der faszinierenden Interferrenzmuster bei der Überlagerung von Schall- oder Lichtwellen. Nach dem Huygenschen Prinzip konnte im Einklang mit der Wellengleichung jeder Punkt einer Wellenfront wieder zum Ausgangspunkt einer Elementarwelle $\psi_i$ werden, jede Wellenfront also aus der Überlagerung aller Elementarwellen gebildet werden: $\psi (\vec{r}, t) = \sum \psi_i (\vec{r}, t)$. Mit der Wellenlänge $\lambda$, der Wellenzahl $k = 2 \pi / \lambda$, der Kreisfrequenz $\omega = 2 \pi \nu$ sowie $c = \lambda \, \nu$, ließ sich als Lösung der Wellengleichung z.B. eine ebene Welle erhalten, die sich in z-Richtung ausbreitet:

$$\psi (z,t) = A \, e^{i(kz-\omega t)}$$

Den Atomismus der Punktmechanik und Strahlungsoptik sowie das Kontinuum der Fluiddynamik und Wellenoptik verband der Astronom Hamilton zu einer genialen Synthese, aus der die Newtonsche Mechanik als geometrisch-optischer Grenzfall einer Wellenbewegung hervorging. Den jeweils aus Elementarwellen gebildeten Wellenfronten konnte er eine geometrische Strahlungsrichtung zuordnen, indem er die Flächen konstanter Wirkung als Wellenfronten ansah, die im Konfigurationsraum fortschritten. Denn so wie sich die Lösungen der Wellengleichung $\psi (az \pm bt)$ nach Ort und Zeit aufspalten ließen, konnte auch die Wirkungsfunktion $S = \int L dt$ separiert werden:

$$S = \int (2T - H)\, dt = \int \vec{p}\, d\vec{r} - Ht = \vec{p}\, \vec{r} - Ht,$$

wenn es sich um eine gleichförmige Bewegung mit Impuls $\vec{p}$ und Gesamtenergie H handelt. Der letzte Ausdruck für die Wirkung S erinnert an die Phase einer Welle: $\phi = \vec{k}\, \vec{r} - \omega t$. Im allgemeineren Fall folgt aus dem Wirkungsintegral:

$$S = \int \vec{p}\, d\vec{r} - Ht = W(\vec{r}) - Ht,$$

so daß $\vec{p} = \vec{\nabla}S = \vec{\nabla}W$ wird und W die charakteristische Funktion bezeichnet. Anschaulich stehen die Impuls-Feldlinien damit senkrecht auf den Flächen gleicher Wirkung; ganz so wie die Strahlen senkrecht auf den Wellenfronten stehen. Hamilton war nichts geringeres als die näherungsweise Vereinheitlichung von Wellen- und Strahlungsoptik gelungen. Der bis heute in der Physik und Naturphilosophie herumgeisternde Welle-Teilchen-Dualismus wurde bereits vor über 150 Jahren von Hamilton gelöst!

Neben den mechanischen Phänomenen der Bewegung von Massen nach dem Prinzip der kleinsten Wirkung, waren es vom Anbeginn der menschlichen Kultur auch die Erscheinungen der Reibungselektrizität (beim Bernstein) und des Magnetismus (von Eisenstein), die die Menschen immer wieder neugierig machten. Ganz zu schweigen von dem gewaltigen Naturschauspiel eines Gewitters, in dem Elektrizität, Licht und Schall aufs innigste zusammenwirken. Goethe hatte es dem Physiker seinerzeit ins Stammbuch geschrieben: Natur ist weder Kern noch Schale. Alles ist mit einem Male.

Coulomb gelang es im Anschluß an Newton, ein dem Gravitationsgesetz ähnliches Kraftgesetz für die Anziehung und Abstoßung zwischen elektrischen Ladungen zu formulieren. Ampere führte den Magnetismus auf das Fließen elektrischer Ströme zurück. Und Faraday sah die Wirkungen der Ladungen aufeinander in der Existenz eines Feldes, dessen Wirkungslinien er durch die Ausrichtung von Eisenfeilspänen zwischen magnetischen Polen veranschaulichte. Maxwell endlich gelang es dann in einem visionären Entwurf, aus den Prinzipien der Ladungs- und Energieerhaltung, Elektrizität und Magnetismus in einer Theorie zu vereinigen. Krönung seiner Elektrodynamik war die Herleitung einer Wellengleichung, nach der Licht als elektromagnetische Welle verstanden werden konnte!

In Verbindung mit der Analyse der diskreten Absorptionslinien im kontinuierlichen Spektrum des Sonnenlichtes, fand Kirchhoff 1859 ein weitreichendes Gesetz zur Strahlungsleistung J eines schwarzen Körper. Aufgrund allgemeiner thermodynamischer Prinzipien konnte er nachweisen, daß die Strahlungsleistung eines schwarzen Körpers allein von der Frequenz $\nu$ und der absoluten Temperatur T abhänge: $J = J(\nu , T)$. Kirchhoff erkannte die Tragweite seines Gesetzes und wies ausdrücklich darauf hin, daß es eine Aufgabe von großer Wichtigkeit sei, diese Funktion zu finden. Aufgrund der enormen experimentellen Schwierigkeiten, konnte das Strahlungsgesetz erst 41 Jahre später durch Planck formuliert werden. Der nächste bedeutende Schritt auf dem Weg zur Quantentheorie gelang Balmer 1885, indem er eine einfache Formel für die Frequenzfolge $\nu_n$ im Emissionsspektrum des Wasserstoffs fand:

$$\nu_n = const. \left({1 \over 4} - {1 \over {n^2}}\right)$$

Die durch Becquerel 1896 entdeckte Radioaktivität gab den Physikern neue Rätsel auf. Wie sollte das um die Jahrhundertwende aufgestellte Zerfallsgesetz $dn = -n\, dW$ interpretiert werden? Das Wahrscheinlichkeitsmaß $dW = \lambda \, dt$ bestimmte durch die Zerfallskonstante $\lambda$ im Zeitintervall dt den Zerfall der Teilchenzahl n im Intervall dn. Was war die Ursache für den spontanen Zerfall der radioaktiven Stoffe?

Die experimentellen Befunde der Schwarzkörperstrahlung, der Atomspektren und der Radioaktivität harrten einer theoretischen Erklärung. Planck und Einstein suchten nach Problemlösungen in der statistischen Mechanik und in der Elektrodynamik. Boltzmann hatte bereits 1877 mit seiner Entropieformel einen Zusammenhang zwischen Makro- und Mikrophysik hergestellt: $S = k\, lnW$. Die Entropie S eines makroskopischen Systems wird danach aus der thermodynamischen Wahrscheinlichkeit W und der heute sogenannten Boltzmannkonstanten k berechnet. W wird dabei durch eine diskrete Abzählmethode zur Verteilung der Energien auf die Teilchen bestimmt. Am wahrscheinlichsten ist ein Zustand mit den meisten Realisierungsmöglichkeiten. Um die gemessene Verteilung der Strahlungsdichte im Hohlraum $u(\nu , T)$ zu verstehen, verteilte Planck um die vorletzte Jahrhundertwende P ununterscheidbare Energiequanten $\epsilon$ über N unterscheidbare elektrische Oszillatoren in den Hohlraumwänden. Er ging von folgenden Annahmen aus: $S_N = k\, lnW$, $U_N = P\epsilon$, W = (N+P-1)! /(n-1)! P!, $S = f(U/\nu )$ und $\epsilon = h\nu$. Heraus kam das mit den Experimenten übereinstimmende Strahlungsgesetz des schwarzen Körpers:

$$u(\nu , T) = {{8\pi h \nu^3}\over {c^3}} {1 \over {e^{{h\nu }\over{kT}} -1}}$$

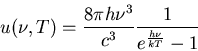
Die Abzählmethode der Statistik enthielt eigentlich schon den Atomismus, der in den diskreten Energiequanten wieder seinen Ausdruck fand. Unverständlich, aber für die Herleitung notwendig, blieb die Annahme der Ununterscheidbarkeit der Energiequanten. Die Lösung dieses Problems gelang später Bose und Einstein.

Die mathematische Struktur der Maxwellschen Elektrodynamik war es, die Einstein 1905 in seiner Arbeit Zur Elektrodynamik bewegter Körper zu seiner speziellen Relativitätstheorie führte. Im Vierervektor-Formalismus der vereinigten Raumzeit konnte die gesamte Elektrodynamik durch eine Gleichung beschrieben werden:

$$\Box {\bf A} = {{4 \pi} \over c} {\bf j}$$

$\Box$ meint den D'Alembert-Operator, ${\bf A}$ das Vierervektor-Potential, dessen Krümmung die elektrischen und magnetischen Feldstärken bestimmt, und ${\bf j}$

steht für die Viererstromdichte. Welch ein Triumpf des NVP! Im Detail blieben aber noch einige Ungereimtheiten. Vor allem die Diskrepanz zwischen den diskreten elektrischen Ladungen und den von ihnen ausgehenden kontinuierlichen elektromagnetischen Wellen ließen den Welle-Teilchen-Dualismus wieder aufleben. Zumal Einstein ebenfalls 1905 im Anschluß an Plancks Entdeckung des Wirkungsquantums Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt nachdachte und darauf hinwies, daß monochromatische Strahlung von geringer Dichte sich wärmetheoretisch so verhielte als ob sie aus voneinander unabhängigen Energiequanten bestünde. Diese Übertragung der Planckschen Quantenhypothese von den elektrischen Oszillatoren in den Hohlraumwänden des schwarzen Körpers auf das elektromagnetische Strahlungsfeld stand in bemerkenswertem Einklang mit der speziellen Relativitätstheorie, in der Einstein die Proportionalität zwischen der Energie und der Frequenz eines Lichtkomplexes hergeleitet hatte: $E = h \nu = \hbar \omega$. Wellenerscheinungen und kontinuierliche Felder waren für Planck und Einstein nur genäherte Mittelwerte über diskrete Teilchenverteilungen. Und so ging es Einstein in seiner dritten Arbeit von 1905 darum, Tatsachen zu finden, welche die Existenz von Atomen von bestimmter endlicher Größe möglichst sicherstellten. Die zufälligen Bewegungen von in ruhender Flüssigkeit suspendierten Teilchen konnte er zur Gänze durch die deterministischen Newtonschen Gesetze erklären! Stochastische Prozesse, wie die zufällige Bewegung suspendierter Teilchen aufgrund der thermischen Bewegung der Wassermoleküle, waren also allein durch Mittelwertbildung über die als kausal geordnet angenommenen Mikrovorgänge erklärbar. 1906 überprüfte Einstein Plancks Ableitung des Strahlungsgesetzes. In seiner Untersuchung Zur Lichterzeugung und Lichtabsorption hob er hervor, daß die Plancksche Theorie implizit von der Lichtquanten-Hypothese Gebrauch machte. Er schrieb: Die Energie eines Elementarresonators kann nur Werte annehmen, die ganzzahlige Vielfache von $h\nu$ sind; die Energie eines Resonators ändert sich durch Absorption und Emission sprungweise, und zwar um ein ganzzahliges Vielfaches von $h\nu$. 1909 äußerte sich Einstein Zum gegenwärtigen Stand des Strahlungsproblems. Im Rahmen der statistischen Mechanik untersuchte er die mittleren quadratischen Energieschwankungen $<\epsilon^2\gt$ einer im thermischen Gleichgewicht befindlichen Strahlungsdichte $\rho$ im Volumen v. Genügte $\rho$ dem Planckschen Gesetz, erhielt er folgendes Ergebnis:

$$<\epsilon^2\gt = \left( h\nu \rho + {{c^3}\over {8\pi \nu^2}} \rho^2 \right) v d\nu$$

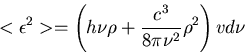
Damit hatte Einstein klar den Doppelcharakter der Wärmestrahlung herausgearbeitet; denn der erste Term in der Klammer steht für den Teilchenanteil und der zweite Term beschreibt den Wellenanteil der Strahlung. Er zog eine programmatische Forderung: Deshalb ist es meine Meinung, daß die nächste Phase der Entwicklung der theoretischen Physik uns eine Theorie des Lichtes bringen wird, welche sich als eine Art Verschmelzung von Undulations- und Emissionstheorie des Lichtes auffassen läßt.

Beim zweiten Versuch, sein Strahlungsgesetz zu verstehen, kam Planck 1911 im Rahmen der statistischen Mechanik zu dem Ergebnis, daß sich die mittlere Energie $<\epsilon \gt$ eines elektrischen Oszillators der Frequenz $\omega$ im Gleichgewicht mit dem Strahlungsfeld der Temperatur T über zwei Terme verteilt:

$$<\epsilon \gt = {{1\over 2} \hbar \omega } + {{\hbar \omega} \over {{e^{{\hbar \omega}\over{kT}}-1}}}$$

Den Ausdruck für T = 0 nannte er Nullpunktsenergie $\epsilon = {1\over 2} \hbar \omega$. Nernst übertrug dann 1913 Plancks Existenzannahme einer Nullpunktsenergie von den materiellen Oszillatoren auf das Strahlungsfeld. Im Anschluß an die Einsteinsche Lichtquanten-Hypothese dachte er sich auch das freie elektromagnetische Feld als aus einer Vielzahl von Energiequanten schwingender Feldoszillatoren zusammengesetzt. Im Grenzübergang zum absoluten Nullpunkt war das Vakuum damit von einem stochastischen Nullpunktsfeld (ZPF) erfüllt.

Bohr versuchte 1913, die Balmerformel zu erklären. Dazu machte er Annahmen über die Struktur der Atome. In seinen Arbeiten zum Aufbau der Atome und Moleküle postulierte er sogenannte stationäre Zustände der Elektronen. Weiter nahm er an, daß Emission und Absorption von Photonen durch sprunghafte Übergänge zwischen solchen Zuständen möglich sein sollten. Er schrieb: Die Energiemenge $\Delta E$, die ausgestrahlt wird bei dem Übergang des Systems aus einem Zustand, der n = n₂, in einen, der n = n₁ entspricht, ist daher unter der Voraussetzung homogener Strahlung mit $\Delta E = E_{n_2} - E_{n_1} = h\, \nu$:

$$\Delta E = {{2 \pi^2 m e^4}\over {h^2}} \left({1\over{n_2}^2} - {1\over{n_1}^2}\right)$$

Wir sehen, daß dieser Ausdruck das Gesetz erklärt, das die Linien in dem Wasserstoffspektrum verbindet. Neben den üblichen Abkürzungen steht m für die Elektronenmasse. Mit dem Geniestreich seiner Quantentheorie hatte Bohr nicht nur die Balmerformel erklärt, sondern den gesamten Aufbau des periodischen Systems der Elemente auf die Beschreibung stationärer Elektronenzustände zurückgeührt. Die Chemie wurde Teilgebiet der Physik!

1917 wandte sich Einstein in seiner Untersuchung Zur Quantentheorie der Strahlung den stochastischen Elementarprozessen zwischen den Molekülen und Lichtquanten zu. Im Anschluß an das Zerfallsgesetz der Radioaktivität nahm er Übergangswahrscheinlichkeiten für Absorptions- sowie für spontane und induzierte Emissionsprozesse an und leitete daraus das Plancksche Strahlungsgesetz ab. Den Strahlungsquanten bei der Wechselwirkung zwischen Feld und Materie schrieb er dabei nicht nur Energien $h\nu$ zu, sondern auch Impulse $h\nu /c$. Im Anschluß an Einstein und unter Rückgriff auf die Hamiltonsche Wirkungswelle konnte dann de'Broglie 1924 die Existenz von Materiewellen postulieren. Mit der Proportionalitätskonstanten $\hbar$ schloß er aus den Phasenbeziehungen für eine Welle $\phi = \vec{k}\, \vec{r} - \omega t$:

$$S = \hbar \phi , \, \, \vec{p} = \hbar \vec{k} , \, \, E = \hbar \omega$$

auf die Wirkungsphase einer Materiewelle gemäß $\phi = S / \hbar$. Denn im Viervektor-Formalismus gilt: $(p_{\mu}) = (E/c, \vec{p}) = \hbar (\omega /c, \vec{k})$.

D.h. aus der Gleichheit der ersten Komponente, die Energie und Frequenz eines Lichtkomplexes in Beziehung setzte, folgerte de'Broglie auch die Gleichheit der weiteren Komponenten, die Impuls und Wellenzahl verknüpften. Was für das Licht galt, sollte fortan für die gesamte Materie gelten! Wie aber sah die Wellengleichung der Materie aus?