,,Damals wie heute suchen viele der bekanntesten Physiker nach einer einheitlichen feldtheoretischen Beschreibung der Natur'' (Lorentz, Poincaré, Wien); denn ,,um 1900 wurde es offensichtlich, daß alle Versuche, die elektromagnetische Theorie im Einklang mit einem mechanistischen Weltbild aus den Gesetzen der Mechanik abzuleiten, wesentlich weniger erfolgreich waren als die von Lorentz 1892 formulierte elektromagnetische Feldtheorie`` (26., S. 91). Wie alle Äthertheoretiker hielt auch Lorentz am Vorhandensein ausgezeichneter Bezugssysteme fest, die im kosmischen Äther ruhten.
Die Äthertheorien gingen auf die Elementenlehre des Aristoteles zurück, bei dem der Äther als Medium der gleichmäßigen Kreisbewegungen der Gestirne fungierte (37., S. 114). Nach Newton'scher Auffassung durchdrang der Äther den absoluten Raum. Im Gegensatz zur Emissionstheorie des Lichtes bezog sich nach undulationstheoretischer Auffassung die Lichtgeschwindigkeit nicht auf den Sender, sondern auf das Medium, den Äther. Innerhalb seines Partikelmodells sprach Newton noch bei der ,,Erklärung'' von Beugungserscheinungen des Lichtes ad-hoc-hypothetisch von Anwandlungen. Hatte Einstein mit seiner Photonenhypothese (siehe unter 4.3) der Newton'schen Lichttheorie zu neuen Ehren verholfen, suchten die Wellenoptiker in Verbindung mit der Ätherhypothese nach einer experimentellen Bestätigung der Existenz des Äthers. Die negativen Ergebnisse aller Ätherdriftexperimente 1. Ordnung erklärte Lorentz 1895 durch eine modifizierte Galilei-Invarianz der Maxwell'schen Gleichungen (26., S. 92), was wiederum einen Widerspruch zur Mechanik bedeutete. Lorentz ergänzte dazu die Galilei-Transformation um eine ,,lokale Zeitkoordinate``:
![]()
wenn, wie üblich, ein System S' mit der Geschwindigkeit v entlang der x-Achse relativ zu S bewegt wird und somit gilt:
![]()
Es sei schon hier hervorgehoben, daß die Gleichsetzung der Zeit:
![]() nur vereinbar mit dem Fernwirkungsprinzip der Newton'schen
Mechanik ist. Ihre Galilei-Invarianz ist dabei im Rahmen der
Bemühungen vieler neuzeitlicher Gelehrter zu sehen, ,,sich in ihren
kosmologischen Theorien von der Vorstellung freizumachen, daß
es im Universum ausgezeichnete Orte gäbe`` (38., S. 641).
nur vereinbar mit dem Fernwirkungsprinzip der Newton'schen
Mechanik ist. Ihre Galilei-Invarianz ist dabei im Rahmen der
Bemühungen vieler neuzeitlicher Gelehrter zu sehen, ,,sich in ihren
kosmologischen Theorien von der Vorstellung freizumachen, daß
es im Universum ausgezeichnete Orte gäbe`` (38., S. 641).
Nachdem 1881 und 1887 die berühmt gewordenen Ätherdriftexperimente in 2. Ordnung von Michelson und Morley (nach Deutung der Äthertheoretiker) fehlgeschlagen waren, führte Lorentz 1895 (wie schon Fitzgerald) als ad-hoc-Hypothese eine Längenkontraktion der Meßapparatur sowie bewegter Elektronen ein (39.). ,,Der Effekt 2. Ordnung, aus dem Vergleich des Hin- und Herganges von Licht für eine Bewegung gegen den Äther und senkrecht zum Äther'', ging auf Maxwell zurück (9., S. 255f):
![]()
![]()
c steht für die Lichtgeschwindigkeit, v für die Erdgeschwindigkeit,
t für die parallele ![]() und senkrechte Laufzeit
und senkrechte Laufzeit ![]() sowie l für den Laufweg des Lichtes.
sowie l für den Laufweg des Lichtes.
Dem Vorschlag Maxwells folgend erwartete Michelson eine
Laufzeitdifferenz: ![]() bzw. mit
den Glgn. 4.4.3/4:
bzw. mit
den Glgn. 4.4.3/4:
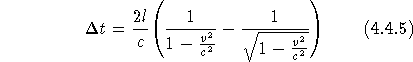
Die Präzisionsmessungen mit einem eigens für die Versuche konstruierten
Interferometer ergaben aber keinen Hinweis auf eine Laufzeitdifferenz,
d.h. ![]() , wobei
, wobei ![]() !
!
Nach der Lorentz-Hypothese verkürzen sich nun Körper, die sich parallel zum Äther bewegen um den Faktor

so daß sich die Laufzeit ![]() vermindert zu:
vermindert zu:
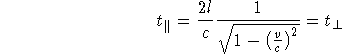
Also ![]() gilt in Übereinstimmung mit dem Experiment
(vgl. 39.).
gilt in Übereinstimmung mit dem Experiment
(vgl. 39.).
In Weiterentwicklung der Theorie formuliert Lorentz 1899 und 1904 gemäß seiner Kontraktionshypothese Transformationen in 2. Ordnung. Die Kontraktion folge dabei aus der Wechselwirkung der gebundenen Elektronen eines mikroskopischen Körpers mit dem Äther. Die Kinematik eines Körpers ergibt sich bei ihm also aus der Dynamik.
Eine mathematisch besonders durchsichtige Darstellung der Lorentz-Transformations-Gruppe sowie der Invarianz der Maxwell-Gleichungen formuliert Poincaré 1905. Die von Lorentz 1899 angegebene Transformation lautet, wenn S' als relativ zu S längs der x-Achse mit v bewegt angenommen wird:
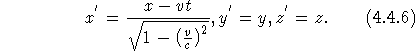
Der Ausdruck für die Zeittransformation wird in der Arbeit von 1904 sinngemäß angegeben mit:
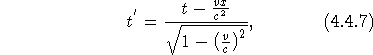
stellt jedoch, ähnlich der modifizierten Galilei-Transformation (vgl. Glgn. 4.4.1/2), nur eine Rechengröße dar (9., S. 259f).
Im Gegensatz zu seinen in ,,empirischer Flickschusterei'' befangenen Zeitgenossen vermied Einstein die Einführung von ad-hoc-Hypothesen; vielmehr suchte er am Maßstab des II. Hauptsatzes nach allgemeinen Prinzipien. Er schrieb später dazu: Schon kurz nach Plancks bahnbrechender Arbeit war mir klar, ,,daß weder die Mechanik noch die Elektrodynamik (außer in Grenzfällen) exakte Gültigkeit beanspruchen können. Nach und nach verzweifelte ich an der Möglichkeit, die wahren Gesetze durch auf bekannte Tatsachen sich stützende konstruktive Bemühungen herauszufinden. Je länger und verzweifelter ich mich bemühte, desto mehr kam ich zu der Überzeugung, daß nur die Auffindung eines allgemeinen formalen Prinzips uns zu gesicherten Erkenntnissen führen könnte. Als Vorbild sah ich die Thermodynamik vor mir. Das allgemeine Prinzip war dort in dem Satze gegeben: die Naturgesetze sind so beschaffen, daß es unmöglich ist, ein perpetuum mobile (erster und zweiter Art) zu konstruieren. Wie aber ein solches allgemeines Prinzip finden?
Ein solches Prinzip ergab sich nach zehn Jahren Nachdenkens aus einem Paradoxon, auf das ich schon mit 16 Jahren gestoßen bin: wenn ich einem Lichtstrahl nacheile mit der Geschwindigkeit c (Lichtgeschwindigkeit im Vakuum), so sollte ich einen solchen Lichtstrahl als ruhendes, räumlich oszillatorisches, elektromagnetisches Feld wahrnehmen. So etwas scheint es aber nicht zu geben, weder auf Grund der Erfahrung noch gemäß den Maxwell'schen Gleichungen. Intuitiv klar schien es mir von vornherein, daß von einem solchen Beobachter aus beurteilt, alles sich nach denselben Gesetzen abspielen müsse wie für einen relativ zur Erde ruhenden Beobachter. Denn wie sollte der erste Beobachter wissen, bzw. konstatieren können, daß er sich im Zustand rascher, gleichförmiger Bewegung befindet?'' (5., S. 19f).
Das Lichtstrahl-Paradoxon führte Einstein in Verbindung mit der Regulationstheorie der Kausalität Humes und der Mach'schen Auffassung von der Gleichwertigkeit aller starren Koordinatensysteme zur Aufgabe des absoluten Characters der Zeit bzw. der Gleichzeitigkeit. Im Zusammenhang mit dem Prinzip von der Konstanz der Lichtgeschwindigkeit gelangte er zur Formulierung des allgemeinen Prinzips der speziellen Relativitätstheorie: ,,die Gesetze der Physik sind invariant mit Bezug auf Lorentz Transformationen. Und er bemerkte weiter: ,,Dies ist ein einschränkendes Prinzip für die Naturgesetze, vergleichbar mit dem der Thermodynamik zugrunde liegenden einschränkenden Prinzip von der Nichtexistenz des perpetuum mobile'' (5., S. 21).
Einstein gehörte um 1905 nicht der Gemeinde der Wissenschaftler an, sondern war als Experte dritter Klasse im Berner Patentamt tätig. Also in Unkenntnis der oben behandelten Arbeiten von Lorentz und Poincaré nahm er sich auf der Grundlage der beiden genannten Prinzipien (Konstanz der Lichtgeschwindigkeit, Relativität) nichts geringeres vor als die Reformulierung der Elektrodynamik. Wie schon Einstein bemerkte (28., S. 29ff), ist das Relativitätsprinzip als Invarianzforderung an physikalische Gesetze grundlegend für jede vereinheitlichende Theorie. Das Prinzip von der Konstanz der Lichtgeschwindigkeit hat demgegenüber selbst dem Relativitätsprinzip zu genügen und läßt sich in Verbindung mit den Gruppeneigenschaften der Bezugsystems-Transformationen sowie mit Homogenitäts- und Isotropie-Forderungen auch aus diesem herleiten (40.). Bei der Ableitung der Lorentz-Transformationen ist im Auge zu behalten, daß die Linearität zwar eine hinreichende, aber keine notwendige Bedingung der Homogenität ist. So lassen sich leicht verallgemeinerte nichtlineare Transformationsgleichungen von 4. Ordng. in v herleiten (55.).
Entgegen vielfacher Lehrbuchauffassungen, die den für den Äthertheoretiker rätselhaften Ausgang des Michelson Versuchs als empirische Grundlage der ihnen andernfalls unglaubwürdigen Relativitätstheorie darstellen, ist mit Holten (12., S. 255ff) hervorzuheben, daß Einsteins Konstruktion der Relativitätstheorie eben prinzipiengeleitet am Maßstab innerer Vollkommenheit orientiert ist und in eher nachgeordneter Weise auf die äußere Bewährung der Theorie abzielt. So beginnt Einstein seine bahnbrechende Arbeit: Zur Elektrodynamik bewegter Körper mit den Worten: ,,Daß die Elektrodynamik Maxwells - wie dieselbe gegenwärtig aufgefaßt zu werden pflegt - in ihrer Anwendung auf bewegte Körper zu Asymmetrien führt, welche den Phänomenen nicht anzuhaften scheinen, ist bekannt. Man denke z.B. an die elektrodynamische Wechselwirkung zwischen einem Magneten und einem Leiter''. Unzufrieden mit inneren Unvollkommenheiten (Asymmetrien der Elektrodynamik), fährt er unter bloß summarischer Erwähnung von Ätherdriftexperimenten fort: ,,Beispiele ähnlicher Art, sowie die mißlungenen Versuche, eine Bewegung der Erde relativ zum Lichtmedium zu konstatieren, führen zu der Vermutung, daß dem Begriffe der absoluten Ruhe ... keine Eigenschaften der Erscheinungen entsprechen''. Unter der Voraussetzung der beiden genannten Prinzipien stellt er dann eine einfache und widerspruchsfreie Elektrodynamik bewegter Körper in Aussicht, die die Einführung eines Lichtäthers überflüssig machen wird (36., S. 891f).
Nach der Art deduktiven Vorgehens behandelt Einstein in einem
kinematischen Teil im Anschluß an eine (operationelle)
Definition der Gleichzeitigkeit die ,,Relativität von Längen und
Zeiten.'' Die Transformationsgleichungen zwischen einem ruhenden
System S und einem relativ zu ihm mit konstanter Geschwindigkeit v
bewegten System ![]() leitet Einstein formal ab, indem er von vornherein
die Relativität der Zeit berücksichtigt. Er schreibt: ,,Zu jedem
Wertsystem x, y, z, t, welches Ort und Zeit eines Ereignisses im ruhenden
System vollkommnen bestimmt, gehört ein jenes Ereignis relativ zum
System
leitet Einstein formal ab, indem er von vornherein
die Relativität der Zeit berücksichtigt. Er schreibt: ,,Zu jedem
Wertsystem x, y, z, t, welches Ort und Zeit eines Ereignisses im ruhenden
System vollkommnen bestimmt, gehört ein jenes Ereignis relativ zum
System ![]() festlegendes Wertsystem
festlegendes Wertsystem ![]() und es
ist nun die Aufgabe zu lösen, das diese Größen verbindende
Gleichungssystem zu finden.'' Die Lösung dieser Aufgabe liefert die
bekannten Gleichungen (vgl. Glgn. 4.4.6/7). Neben der Verkürzung
bewegter Maßstäbe weist Einstein explizit auf die physikalische
Bedeutung der Relativität der Zeit hin, daß nämlich
bewegte Uhren langsamer gingen (36., S. 903f).
und es
ist nun die Aufgabe zu lösen, das diese Größen verbindende
Gleichungssystem zu finden.'' Die Lösung dieser Aufgabe liefert die
bekannten Gleichungen (vgl. Glgn. 4.4.6/7). Neben der Verkürzung
bewegter Maßstäbe weist Einstein explizit auf die physikalische
Bedeutung der Relativität der Zeit hin, daß nämlich
bewegte Uhren langsamer gingen (36., S. 903f).
Nach Ableitung des Additionstheorems der Geschwindigkeiten zeigt er im elektrodynamischen Teil zunächst die Invarianz der Maxwell-Gleichungen bzgl. der hergeleiteten Lorentz-Transformationen. Danach ist ihm klar, ,,daß die in der Einleitung angeführte Asymmetrie bei der Betrachtung der durch Relativbewegung eines Magneten und eines Leiters erzeugten Ströme verschwindet'' (36., S. 909). Weiter behandelt er die Theorie des Doppler'schen Prinzips und der Aberation und wendet sich der Transformation der Energie der Lichtstrahlen zu. Nachdem er die Transformationsgleichung:
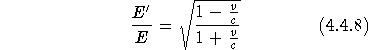
hergeleitet hat, hebt er hervor: ,,Es ist bemerkenswert, daß die Energie und die Frequenz eines Lichtkomplexes sich nach demselben Gesetze mit dem Bewegungszustande des Beobachters ändern'' (36., S. 913). Dieses Bemerkenswerte ist in Verbindung mit Einsteins Photonenhypothese zu würdigen; denn mit der Frequenztransformation nach dem Doppler'schen Prinzip folgt:
![]()
also die Proportionalität von E und ![]() .
.
Nachdem Einstein fürderhin die Lorentz-Invarianz der Ladungserhaltung gefolgert hat, macht er Ausführungen zur ,,Dynamik des (langsam beschleunigten) Elektrons.'' Für die Bewegungsenergie T des Elektrons erhält er:
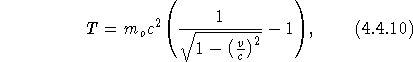
wobei ![]() die Ruhemasse des Elektrons und v seine Geschwindigkeit
bezeichnet.
die Ruhemasse des Elektrons und v seine Geschwindigkeit
bezeichnet.
In einer ergänzenden Arbeit unter dem Titel: ,,Ist die Trägheit eines
Körpers von seinem Energiegehalt abhängig?'' (41.) leitet Einstein
dann, anknüpfend an die Beziehung der Energietransformation (Glg. 4.4.8),
die weitreichende Folgerung ab: ,,Die Masse eines Körpers ist ein
Maß für dessen Energieinhalt``; ändert sich die Energie um E,
so ändert sich die Masse in demselben Sinne um ![]() , d.h.:
, d.h.:
![]()
![]()
Einstein gibt wiederum einen Hinweis zur Bestätigung seiner Folgerung: ,,Es ist nicht ausgeschlossen, daß bei Körpern, deren Energieinhalt in hohem Maße veränderlich ist (z.B. bei den Radiumsalzen), eine Prüfung der Theorie gelingen wird.``
Bevor wir in groberer Skizze als bisher einige Gedanken zur allgemeinen Relativitätstheorie formulieren, seien noch einmal wichtige Unterschiede in der Behandlung der Elektrodynamik durch Einstein und Lorentz stichwortartig zusammengefaßt:
Im Gegensatz zu a) und b) werden die unter c) und d) genannten Problembereiche nach wie vor diskutiert (42., 43., S. 84ff, 44., 45.).
Next: Zur allgemeinen Relativitätstheorie Up: Zur Krisenbewältigung in der Previous: Über einen die Erzeugung
Ingo Tessmann