Quantisierung und Geometrisierung haben zu einer faszinierenden, näherungsweise vereinheitlichten
Theorie geführt, dem Standard-Modell. Eine supersymmetrische Vereinigung von ART und QFT ist
allerdings erst im Bereich der Planckenergie von ![]() zu erwarten und damit astronomisch
weit von den experimentell zugänglichen Energien bei
zu erwarten und damit astronomisch
weit von den experimentell zugänglichen Energien bei ![]() entfernt. Aufgrund mangelnder
empirischer Prüfbarkeit kommt der Sorgfalt beim Entwurf der Forschungsprogramme, ihrer ersten
Prinzipien und der mathematischen Ausformulierung besondere Bedeutung zu.
entfernt. Aufgrund mangelnder
empirischer Prüfbarkeit kommt der Sorgfalt beim Entwurf der Forschungsprogramme, ihrer ersten
Prinzipien und der mathematischen Ausformulierung besondere Bedeutung zu.
Im Forschungsprogramm
der klassischen Physik war die Natur selbst zum Gegenstand der Untersuchung auserkohren worden.
Von der Beschreibung der Planetenbahnen durch Kepler bis hin zur Kosmologie Einsteins, ging es
um ein rationales Verständnis der beobachtbaren Naturvorgänge. Die Natur wurde dabei als an sich
seiend unterstellt, die unabhängig davon existierte, ob es Menschen gab, die sie untersuchten.
Die Naturforscher folgten einer realistischen Weltsicht mit dem Ziel einer objektiven Erklärung der
Naturereignisse. Die Grundvorgänge wurden als kausal und deterministisch geordnet angenommen.
Die statistischen Methoden der Thermodynamik änderten nichts am Prinzip der Ordnung auch auf
dem atomaren Beschreibungsniveau. Lediglich das menschliche Unvermögen, die astronomische Vielfalt
in der Bewegung von 1023 Teilchen zu verfolgen, zwang zu statistischen Mittelwertbildungen und
Schwankungsberechnungen. Die makroskopischen Sterne, Planeten und Asteroiden konnten anhand ihrer
Bewegungsverläufe identifiziert und durch Zustandsbeschreibungen charakterisiert werden, so daß
weitreichende Extrapolationen in Vergangenheit und Zukunft möglich waren. Hinsichtlich der
Myriaden von Sternen und Galaxien sowie der unzähligen schwarzen Materie im gesamten Kosmos war
die Situation allerdings ganz ähnlich wie auf dem atomaren Niveau. Analog zur Thermodynamik
eines abgeschlossenen Systems wurde die Einsteinsche Feldgleichung zu einer Zustandsgleichung
der Raumzeit umformuliert. So wie z.B. Druck und Temperatur das Volumen eines Gases bestimmen,
legen Energie und Impuls die Geometrie der Raumzeit fest.
Im Forschungsprogramm der modernen Physik ist die Natur selbst nicht mehr als
Forschungsgegenstand erhalten geblieben. Das atomare Naturgeschehen wurde nur noch insoweit
untersucht, wie es sich zeigte, wenn es mit realisierbaren Meßgeräten registriert werden konnte.
Die Alltagsrationalität, die der menschlichen Erfahrung mit wahrnehmbaren und handhabbaren
Dingen und Vorgängen der Umwelt erwuchs, wurde als unzureichend überwunden. Der Natur
wurde keine eigene Seinsweise mehr unterstellt, sondern ihre Erkennbarkeit durch den Menschen
stand im Vordergrund. Die Naturforscher folgten einer positivistischen Weltsicht mit dem Ziel
einer subjektgebundenen Erklärung der Naturerscheinungen. Die Grundvorgänge wurden als
zufällig und indeterminiert angenommen. Im Gegensatz zu den statistischen Methoden der
Thermodynamik bezogen sich die Quantenstatistiken bereits auf einzelne Teilchen, deren Zustände
aufgrund der prinzipiellen Meßwechselwirkungen fluktuierten. Die mikroskopischen Elementarteilchen
konnten nur noch in Abhängigkeit technisch aufwendiger Experimente in Zustände versetzt werden,
die kaum mehr Extrapolationen im Rahmen der sich ausweitenden Wahrscheinlichkeitsverteilungen
zuließen. Weitreichende Zustandsbeschreibungen waren nicht mehr möglich. Vielmehr wurden die
Meßoperationen beim Experimentieren als Operatoren in die Theorie aufgenommen. Mit dem Aufbau
des Experiments wurde überhaupt erst festgelegt, welche Zustände möglich waren bzw. welche
Eigenschaften die Atome haben konnten. Da es bei Meßoperationen, wie bei allen Handlungen,
im allgemeinen auf die Reihenfolge ankommt, wurde dem atomaren Zustandsraum die nichtkommutative
Struktur der Operatorenalgebra aufgeprägt: ![]() . Diese Vertauschungsrelation
bildet den theoretischen Kern der gesamten modernen Physik.
. Diese Vertauschungsrelation
bildet den theoretischen Kern der gesamten modernen Physik.
Im Forschungsprogramm der neoklassischen Physik geht es darum, die Prinzipien der klassischen Physik wiederzubeleben und auch die Mikrophysik in natürlicher Weise der Alltagsrationalität zugänglich zu machen. Nicht das Trennende zwischen klassischer und moderner Physik gilt es herauszuarbeiten, sondern das Gemeinsame wird im Vordergrund stehen. Folgende Parolen sollen als Richtlinien dienen, um zu sehen, wie weit die klassischen Prinzipien zwingend abgeschwächt werden müssen bzw. um zu prüfen, ob sie nicht vielleicht auch überzogen sind:
Wie weit das Festhalten bzw. Wiedererlangen der klassischen Prinzipien reichen wird, soll am Beispiel dreier Theorien näher ausgeführt werden: der Bohmschen Mechanik , der stochastischen Elektrodynamik und der Quantengravitation . Unzufrieden mit dem Positivismus Bohrs und Heisenbergs geht es Bohm im Anschluß an die Einsteinsche Arbeit zur Unvollständigkeit der Quantenmechanik darum, die Quantentheorie wieder aus klassischen Prinzipien heraus zu verstehen. 1952 tritt er mit zwei Arbeiten hervor: A suggested interpretation of the quantum theory in terms of ``hidden'' variables, I and II. Er beginnt mit den Worten: The usual interpretation of the quantum theory is self-consistent, but it involves an assumption that cannot be tested experimentally, that the most complete possible specification of an individual system is in terms of a wavefunction that determines only probable results of actual measurement processes. Demgegenüber stellt er in Aussicht, that it is not necesarry for us to give up a precise, rational, and objective description of individual systems at a quantum level of accuracy. Seine physikalische Interpretation der Schrödingergleichung beginnt mit dem Ansatz:
![]()
![]()
Das Geschwindigkeitsfeld ![]() folgt dabei aus dem Gradienten der Wirkungsfunktion S:
folgt dabei aus dem Gradienten der Wirkungsfunktion S:
![]()
![]()
Im Gegensatz zu Heisenberg nimmt Bohm die objektive Existenz der Teilchenbahnen
![]() an, die nicht erst dadurch entstünden, daß wir sie beobachteten. Die
Statistik des Quantenpotentials ist nach Bohm lediglich die Konsequenz unserer Unkenntnis
der genauen Anfangsbedingungen der Teilchenbahnen. Unter folgenden drei Annahmen folgt die
Quantenmechanik aus der Bohmschen Mechanik:
an, die nicht erst dadurch entstünden, daß wir sie beobachteten. Die
Statistik des Quantenpotentials ist nach Bohm lediglich die Konsequenz unserer Unkenntnis
der genauen Anfangsbedingungen der Teilchenbahnen. Unter folgenden drei Annahmen folgt die
Quantenmechanik aus der Bohmschen Mechanik:
Bohm hatte durch Herleitung einer Newtonschen Bewegungsgleichung für die Teilchenorte im
Konfigurationsraum eine realistische Interpretation der Quantentheorie erreicht. Die
Existenz des nichtlokalen Quantenpotentials allerdings blieb für Einstein weiterhin
ein Stein des Anstoßes.
1964 griff Bell das Problem der quantenmechanichsen Unvollständigkeit auf. In seiner
Untersuchung
On the Einstein-Podolsky-Rosen paradox konnte er zeigen, daß jede
Ergänzung der Quantentheorie um lokale verborgene Variable den statistischen
Vorhersagen der Quantenmechanik widersprach. Für eine Realisierung des Einsteinschen
Gedankenexperiments nahm er Spinmessungen an zwei von einander separierten Teilchen eines
gemeinsames Spin-Zustandes an. Als verborgene Variable setzte er einen beliebigen
Parameter ![]() an, von dem die Resultate der Messungen A und B der
Spin-Zustände
an, von dem die Resultate der Messungen A und B der
Spin-Zustände ![]() und
und ![]() abhängen konnten:
abhängen konnten:
![]() ,
, ![]() . Als wesentliche Annahme
setzte Bell die jeweilige statistische Unabhängigkeit der Meßergebnisse von A und
B voraus. Mit der Wahrscheinlichkeitsdichte
. Als wesentliche Annahme
setzte Bell die jeweilige statistische Unabhängigkeit der Meßergebnisse von A und
B voraus. Mit der Wahrscheinlichkeitsdichte ![]() erhielt er für den
Erwartungswert
erhielt er für den
Erwartungswert ![]() des Produktes der beiden Spin-Komponenten
des Produktes der beiden Spin-Komponenten
![]() und
und ![]() :
:
![]()
![]()
![]()
Seitdem erstmals 1982 die Gültigkeit der Quantenmechanik im Gegensatz zu einer
Theorie mit lokalen verborgenen Parametern experimentell bestätigt werden
konnte, galt Einstein als widerlegt und die Kopenhagener Deutung erhielt ungeheuren
Auftrieb. Kaum jemand hatte allerdings zur Kenntnis genommen, daß Bells Ungleichung
zwar eine Erweiterung der Quantenmechanik um lokale Parameter ausschloß, die
nichtlokalen verborgenen Ortsvariablen der Bohmschen Mechanik aber unberührt ließ.
Für Realisten blieb die Bohmsche Mechanik als Grundlage der Quantenmechanik weiterhin attraktiv. Und so stellt Dürr in seinem gleichnamigen Lehrbuch eine neue Theorie für die Bewegung von Teilchen auf, die in gewissem Sinne minimal ist, die die Galileische Raum-Zeit-Symmetrie respektiert und die die Newtonsche Mechanik als Näherung enthält. Die statistische Mechanik dieser Theorie liefert in idealisierten Situationen den quantenmechanischen Formalismus zur Beschreibung der statistischen Ausgänge von Experimenten. Für ein N-Teilchensystem mit Massen mk und Orten qk im Konfigurationsraum gelten folgende Gleichungen:
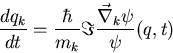
dqk/dt bestimmt das Geschwindigkeitsfeld ![]() und
und ![]() gehorcht
der Schrödingergleichung:
gehorcht
der Schrödingergleichung:
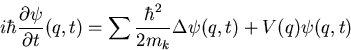
![]()
![]()
Unter der Annahme der Äquivarianz von Wahrscheinlichkeitsmaß und
Geschwindigkeitsfeld formuliert Dürr die Quantengleichgewichtshypothese,
nach der das Bornsche statistische Gesetz gilt: ![]() . In Analogie
zur Boltzmann-Verteilung:
. In Analogie
zur Boltzmann-Verteilung: ![]() ist die Bohmsche Mechanik
eine statistische Mechanik zur Quantenmechanik. Für Dürr ist sie die minimale
Vervollständigung der Schrödingerschen Theorie, die darin bestehe, daß
wir auch ,,Teilchen`` meinen, wenn wir ,,Teilchen`` sagen.
ist die Bohmsche Mechanik
eine statistische Mechanik zur Quantenmechanik. Für Dürr ist sie die minimale
Vervollständigung der Schrödingerschen Theorie, die darin bestehe, daß
wir auch ,,Teilchen`` meinen, wenn wir ,,Teilchen`` sagen.
Die Bohmsche Mechanik als statistische Mechanik der Quantenmechanik erfüllt alle Bedingungen, die an eine klassische Theorie zu stellen sind. Sie nimmt die reale Existenz von Teilchen an, denen in objektiver Weise Orte und Geschwindigkeiten, Massen und Ladungen, Impulse und Energien zugeordnet werden können. Damit ist die Bohmsche Mechanik eine realistische und objektive Seinslehre. Die Entwicklungsgleichungen für das Führungs- und Geschwindigkeitsfeld sind kausal und deterministisch. D.h. fixierte Anfangs- und Randbedingungen legen den zeitlichen Verlauf des Führungsfeldes und der Teilchenorte fest. Die Quantengleichgewichtshypothese trägt lediglich dem Umstand Rechnung, daß die Anfangs- und Randbedingungen für Mikroobjekte nicht beliebig genau angebbar sind. Und in Analogie zur Boltzmannkonstanten k handelt es sich bei der Planckkonstanten h bloß um einen Skalierungsfaktor zwischen Mikro- und Makrophysik.
Warum hat sich die Bohmsche Einsicht bisher nicht durchsetzen können? Sie wurde im Ansatz bereits 1927 von de`Broglie formuliert. Was machte die orthodoxe Quantenmechanik demgegenüber so attraktiv? Wirkten sich ähnlich wie auf die kritische Theorie die politischen Verhältnisse der Weimarer Republik auf das Theorienverständnis aus? War es die Komplementaritäts-Philosophie und vor allem die überragende Persönlichkeit Bohrs , die der Quantenmechanik ihren prägenden Stempel aufdrückte? Oder dominierten eher innerphysikalische Gründe die Ignoranz gegenüber Alternativen? Die Bohmsche Mechanik ist aufgrund ihrer Nichtlokalität nicht Lorentz-invariant. Das ist die orthodoxe Quantenmechanik auch nicht. Wie ist die Lokalität der QFT damit zu vereinbaren? Nach Mack ist die Nichtlokalität lediglich ein Definitionskriterium für Emergenz. D.h. nichtlokale Effekte sollen letztlich aus lokalen Wechselwirkungen im Rahmen einer verallgemeinerten Eichtheorie verstanden werden können. Das ist bisher noch Programm. Ebenso unvollendet ist der Versuch einer Vereinheitlichung von ART und QFT geblieben.
Bell und Goldstein
haben wiederholt darauf hingewiesen, daß eine am Meßverfahren orientierte
Theorie in der Kosmologie keinen Sinn mache. Vielmehr sei es gerade die
objektiv-realistische Behandlung der Teilchenorte und des Führungsfeldes
![]() innerhalb der Bohmschen Mechanik, die eine naheliegende Verbindung
mit der ART erlaube, indem die Ortskoordinaten zur Metrik und das Bohmsche
Führungsfeld zum Materiefeld verallgemeinert würden:
innerhalb der Bohmschen Mechanik, die eine naheliegende Verbindung
mit der ART erlaube, indem die Ortskoordinaten zur Metrik und das Bohmsche
Führungsfeld zum Materiefeld verallgemeinert würden: ![]() .
In seiner Arbeit Ontological clarity and the conceptual foundations of Quantum Gravity
formuliert Goldstein im Anschluß an das Verfahren der kanonischen Quantisierung einen
ähnlichen Zusammenhang für die Metrik wie Dürr für die Orte:
.
In seiner Arbeit Ontological clarity and the conceptual foundations of Quantum Gravity
formuliert Goldstein im Anschluß an das Verfahren der kanonischen Quantisierung einen
ähnlichen Zusammenhang für die Metrik wie Dürr für die Orte:
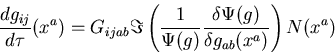
Die Wheeler-DeWitt-Gleichung der Quantenkosmologie bestimmt ![]() und übernimmt
die Rolle der Schrödinger-Gleichung. Gijab steht für die Supermetrik, die eine
Funktion der Metrik ist. Und N(xa) bezeichnet die sogenannte Lückenfunktion, die von der
Wahl der Hyperflächen-Schichtung abhängt. Ihre Eindeutigkeit ist noch ein offenes Problem.
In der Quantengravitation wird die allgemein-relativistische Invarianz der vierdimensionalen
Raumzeit durch eine zeitliche Schichtung dreidimensionaler Ortsräume dargestellt.
Analog zur lokalen Annäherung des gekrümmten Riemannschen Raumes durch den Minkowskiraum
in der ART kann die Hyperflächen-Schichtung der Quantengravitation durch eine
Relativzeit-Invarianz der Bohmschen Mechanik für den Labormaßstab angenähert
werden. Wie Bell in Verbindung mit der Frage Are there quantum jumps? hervorhebt,
ist die Relativzeit-Invarianz als Näherung der Lorentz-Invarianz im Rahmen einer
nichtrelativistischen Theorie auffaßbar. Zudem könnten, wie beim Konzept der
Symmetriebrüche im Standard-Modell, die abgeschwächten Raumzeit-Invarianzen als
Symmetriebrüche im Rahmen der Quantengravitation verstanden werden.
und übernimmt
die Rolle der Schrödinger-Gleichung. Gijab steht für die Supermetrik, die eine
Funktion der Metrik ist. Und N(xa) bezeichnet die sogenannte Lückenfunktion, die von der
Wahl der Hyperflächen-Schichtung abhängt. Ihre Eindeutigkeit ist noch ein offenes Problem.
In der Quantengravitation wird die allgemein-relativistische Invarianz der vierdimensionalen
Raumzeit durch eine zeitliche Schichtung dreidimensionaler Ortsräume dargestellt.
Analog zur lokalen Annäherung des gekrümmten Riemannschen Raumes durch den Minkowskiraum
in der ART kann die Hyperflächen-Schichtung der Quantengravitation durch eine
Relativzeit-Invarianz der Bohmschen Mechanik für den Labormaßstab angenähert
werden. Wie Bell in Verbindung mit der Frage Are there quantum jumps? hervorhebt,
ist die Relativzeit-Invarianz als Näherung der Lorentz-Invarianz im Rahmen einer
nichtrelativistischen Theorie auffaßbar. Zudem könnten, wie beim Konzept der
Symmetriebrüche im Standard-Modell, die abgeschwächten Raumzeit-Invarianzen als
Symmetriebrüche im Rahmen der Quantengravitation verstanden werden.
Die orthodoxe Quantenmechanik ist auf die experimentelle Situation im Labor zugeschnitten. Dieser im Vergleich mit der Kosmologie eher bescheidene Anspruch ist der Hauptgrund für die instrumentalistische Sichtweise und die positivistische Philosophie. Entsprechend wird die Wellenfunktion nicht als Wirkungs- oder Führungsfeld angesehen, sondern lediglich als Wissensreservoir oder Information interpretiert. Die durch das Wahrscheinlichkeitsmaß beschriebene Zufälligkeit der Grundvorgänge beim radioaktiven Zerfall wie bei der spontanen Emission von Lichtquanten wird dem Meßeingriff in Verbindung mit der experimentellen Situation zugeschrieben. Demgegenüber sehen die Physiker mit objektiver Sichtweise und realistischer Philosophie den Grund der Zufälligkeit in den Naturvorgängen selbst. Sie unterstellen eine objektive Existenz stochastischer Prozesse. Eine Zwischenposition nimmt die Ensemble-Interpretation der Wahrscheinlichkeit in der statistischen Mechanik ein. Man gerät allerdings in Schwierigkeiten, wenn man sie auf das Universum als Ganzes anzuwenden versucht. Alternative Quantentheorien auf der Basis stochastischer Prozesse wurden bereits Ende der 1920er Jahre vorgeschlagen. Versuche einer klassischen Alternative zur QED werden unter dem Titel stochastische Elektrodynamik (SED) verfolgt. Als Ursache der stochastischen Prozesse werden die reale Existenz der ZPE und des ZPF angesehen. In der QED dagegen ist die ZPE lediglich das Reservoir virtueller Quanten im Rahmen der Unbestimmtheitsrelationen.
Die SED geht aus von der Planckschen Entdeckung der ZPE bei der Analyse seiner
Strahlungsformel. Danach setzt sich die spektrale Energiedichte ![]() zusammen aus dem Produkt
zusammen aus dem Produkt ![]() der Zahl der Eigenschwingungen im Einheitsvolumen
und der mittleren Energie
der Zahl der Eigenschwingungen im Einheitsvolumen
und der mittleren Energie ![]() der Feldoszillatoren der Frequenz
der Feldoszillatoren der Frequenz ![]() .
Mit
.
Mit ![]() und
und ![]() folgt für
folgt für
![]() :
:
![]()
Damit ist die Planckkonstante als Intensitätsmaß für die Fluktuationen des ZPF
eingeführt worden. Ähnlich wie die Boltzmannkonstante als Intensitätsmaß für
die Wärmeschwankungen angesehen werden kann. Als Zufallsvariablen des ZPF erweisen
sich die Amplituden ![]() , z.B. in der Entwicklung
des Vektorpotentials
, z.B. in der Entwicklung
des Vektorpotentials ![]() nach ebenen Wellen im Volumen V:
nach ebenen Wellen im Volumen V:
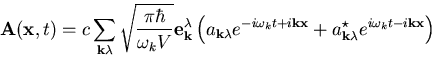
![]() meint den Wellenvektor und
meint den Wellenvektor und ![]() den Polarisationsindex. Für die Amplituden
gilt natürlich im Mittel:
den Polarisationsindex. Für die Amplituden
gilt natürlich im Mittel: ![]() . Werden die Untersuchungen
des ZPF auf das thermische Gleichgewicht des Strahlungsfeldes ausgedehnt, ergibt sich auch
das Verteilungsgesetz <ni>B der Bosestatistik. Und zwar ohne die Existenzannahme diskreter
Lichtquanten. Denn beim ZPF handelt es sich im Prinzip um ein kontinuierliches Maxwellfeld,
dessen Amplituden eine Zufallsmenge bilden.
. Werden die Untersuchungen
des ZPF auf das thermische Gleichgewicht des Strahlungsfeldes ausgedehnt, ergibt sich auch
das Verteilungsgesetz <ni>B der Bosestatistik. Und zwar ohne die Existenzannahme diskreter
Lichtquanten. Denn beim ZPF handelt es sich im Prinzip um ein kontinuierliches Maxwellfeld,
dessen Amplituden eine Zufallsmenge bilden.
Zudem werden die Einsteinschen
Übergangswahrscheinlickkeiten bei der Absorption sowie der spontanen und induzierten
Emission als ZPF-Effekte verständlich. Auch Streuungseffekte wie der Compton-Effekt sind
ohne Quantisierungsannahmen berechenbar. Und als Umgebungseffekte des ZPF erweisen sich
der Casimier-Effekt, die Van der Waals - Kräfte und der Unruh-Effekt. Last but not least
läßt sich die träge Masse
aus
der Gegenwirkung des ZPF beim Beschleunigen von Objekten verstehen. Aufgrund des
Äquivalenzprinzips wäre die Masse damit schlechthin auf ZPE zurückgeführt. Der Clou dabei
ist die instantane Allgegenwart des Vakuums. Da das ZPF Lorentz-invarinat ist, scheint
der Einsteinsche Traum von einer lokalen und realistischen Theorie verwirklichbar zu sein.
Auch die Annahme der statistischen Unabhängigkeit als Voraussetzung der Bellschen Ungleichung
erscheint im Rahmen der SED nicht mehr zwingend.
Schwierigkeiten ergeben sich allerdings mit der Anzahl der Eigenschwingungen im ZPF, die
jeweils den Energiebeitrag von ![]() enthalten und im Prinzip mit
beliebig hoher Frequenz auftreten können. D.h. die Gesamtenergie des Vakuums strebte gegen
unendlich und als Beitrag zum Einsteinschen Energie-Impuls-Tensor wäre die Auswirkung
auf die Raumkrümmung so groß, daß das Universum sofort im Unendlichen verschwände.
Trägt das ZPF also überhaupt zur Gravitation bei? Wo läge die cutoff - Frequenz
einer sinnvollen Theorie? Bei der Planckfrequenz
enthalten und im Prinzip mit
beliebig hoher Frequenz auftreten können. D.h. die Gesamtenergie des Vakuums strebte gegen
unendlich und als Beitrag zum Einsteinschen Energie-Impuls-Tensor wäre die Auswirkung
auf die Raumkrümmung so groß, daß das Universum sofort im Unendlichen verschwände.
Trägt das ZPF also überhaupt zur Gravitation bei? Wo läge die cutoff - Frequenz
einer sinnvollen Theorie? Bei der Planckfrequenz ![]() oder eher bei der Comptonfrequenz
oder eher bei der Comptonfrequenz
![]() ? Fairerweise muß angemerkt werden, daß Divergenzprobleme auch in der QED
auftreten. Dort sind ausgeklügelte Renormierungsverfahren entwickelt worden, um
die Ergebnisse der Theorie mit den prinzipiell immer endlichen Resultaten der Experimente
vergleichen zu können. Warum das mit einer unglaublichen Genauigkeit von bis zu 12 Stellen
gelingt, ist noch weitgehend unverstanden. In der SED tritt weiterhin das Problem auf, schon
beim Verständnis eines so einfachen Systems wie dem Wasserstoffatom zu scheitern; denn das
isolierte H-Atom ist innerhalb der SED instabil. Da isolierte Betrachtungen einzelner
Atome allerdings höchst künstlich sind, hat das Scheitern eher Erkenntniswert. Zudem weisen
astronomische Untersuchungen darauf hin, daß freie H-Atome im All in der Tat nicht stabil
sind. Die jeweilige Umgebung scheint also wesentlich zur Stabilität beizutragen. Der in den
instantanen Quantenkorrelationen aufscheinende Holismus könnte in der realen Existenz des
ZPF seine Erklärung finden. Es sind noch bei weitem nicht alle Ergebnisse der QED in der
SED nachvollzogen worden. Insbesondere bei nichtlinearen Effekten höherer Ordnung versagt
die SED. De la Pena und Cetto weisen in ihrem Buch The Quantum Dice im Ausblick
darauf hin, daß die SED letztlich zu einer schon im Ansatz nichtlinearen Theorie komplexer
Systeme erweitert werden müßte.
? Fairerweise muß angemerkt werden, daß Divergenzprobleme auch in der QED
auftreten. Dort sind ausgeklügelte Renormierungsverfahren entwickelt worden, um
die Ergebnisse der Theorie mit den prinzipiell immer endlichen Resultaten der Experimente
vergleichen zu können. Warum das mit einer unglaublichen Genauigkeit von bis zu 12 Stellen
gelingt, ist noch weitgehend unverstanden. In der SED tritt weiterhin das Problem auf, schon
beim Verständnis eines so einfachen Systems wie dem Wasserstoffatom zu scheitern; denn das
isolierte H-Atom ist innerhalb der SED instabil. Da isolierte Betrachtungen einzelner
Atome allerdings höchst künstlich sind, hat das Scheitern eher Erkenntniswert. Zudem weisen
astronomische Untersuchungen darauf hin, daß freie H-Atome im All in der Tat nicht stabil
sind. Die jeweilige Umgebung scheint also wesentlich zur Stabilität beizutragen. Der in den
instantanen Quantenkorrelationen aufscheinende Holismus könnte in der realen Existenz des
ZPF seine Erklärung finden. Es sind noch bei weitem nicht alle Ergebnisse der QED in der
SED nachvollzogen worden. Insbesondere bei nichtlinearen Effekten höherer Ordnung versagt
die SED. De la Pena und Cetto weisen in ihrem Buch The Quantum Dice im Ausblick
darauf hin, daß die SED letztlich zu einer schon im Ansatz nichtlinearen Theorie komplexer
Systeme erweitert werden müßte.
Die Ansicht, daß kontinuierliche Felder in Verbindung mit dem Atomismus nur jeweils genäherte Mittelwerte über endliche Volumina sein können, vertrat schon Einstein. Und bereits 1924 nahm er die Existenz zufälliger Fluktuationen des metrischen Tensors an, um die Beschreibung eines wirklichen, allgegenwärtigen Materiefeldes zu ermöglichen. Dabei galt ihm jegliches Indiz für Zufälligkeit als Anzeichen einer statistisch-näherungsweisen Beschreibung der exakt-geordneten Grundvorgänge. Nicht nur die ART, sondern auch die QFT sind demnach lediglich effektive Theorien auf mittlerem Beschreibungsniveau. Die Mehrzahl der Theoretiker nimmt Quantenfluktuationen auch auf dem Niveau der Plancklänge an:
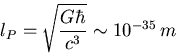
Objektiv-stochastische Theorien des Universums werden von Sidharth aus den
Fluctuations in the Quantum Vacuum
entwickelt sowie im Rahmen einer allgemeinen
Prozessphysik
aus den
Iterationen eines selbstbezüglichen Rauschens (SRN) zu formulieren versucht. Danach sind
Ordnungsstrukturen im Kosmos die seltenen Ausnahmen und von flüchtiger Vergänglichkeit.
Diese Weltsicht wird in verblüffender Weise gestützt durch Einsichten der Zahlentheorie.
Die Berechnung der Haltewahrscheinlichkeit einer universalen
Turing-Maschine
hat nämlich gezeigt,
daß sie gleichbedeutend mit reinem Zufall ist, also nicht vom idealen Münzwurf unterschieden werden
kann. Beweise sind die höchst seltene Ausnahme, Wahrheiten ohne Gründe, Ereignisse ohne Ursache der
astronomisch häufige Regelfall.
Zu den Ausnahmen unter den Physikern, die nach wie vor eine realistisch-deterministische Beschreibung des Universums im Rahmen einer vereinheitlichten Theorie der Quantengravitation für möglich halten, gehört `t Hooft . In seinem populären Buch In search of the ultimate building blocks hebt er hervor: The history books say that Bohr has proved Einstein wrong. But others, including myself, suspect that in the long run, the Einsteinian view might return. Unterdessen ist er mit mehreren Arbeiten hervorgetreten, in denen er die Quantengravitation als dissipativ deterministisches System untersucht. Er schreibt: A theory is developed that will not postulate the quantum states as being its central starting point, but rather classical deterministic degrees of freedom. Quantum states, being mere mathematical devices enabling physicists to make statistical predictions, will turn out to be derived concepts, with a not strictly locally formulated definition. Und ganz im Sinne Einsteins, Chaos aus einer unterliegenden Schicht der Ordnung zu erklären, formuliert `t Hooft die Perspektive: It may still possible that the quantum mechanical nature of the phenomenological laws of nature at the atomic scale can be attributed to an underlying law that is deterministic at the Planck scale but with chaotic effects at all larger scales.