Next: Ludwig Wittgenstein Up: Die Rätsel der Welt Previous: Paradoxien und Grundlagenkrisen

Bertrand Russell

Der nächste Morgen begann wie gewohnt. Nach einer erfrischenden Dusche und ausgiebigem Frühstück machten sich die beiden an die Planung des Tagesablaufs. Sie beschlossen, mit den Fragen zu beginnen.

,,Daß Axiome ihrer Folgesätze wegen geglaubt werden sollen, war auch Hilberts Ansicht``, erinnerte sich Hilde.

,,Mit dem Glauben wird wohl die Willkür bei der Setzung der Axiome angedeutet``, ergänzte Sofie. ,,Aber was sind logische Atome? Wenn wir an die Legosteine denken, können wir versuchen, sie in Analogie zu den physikalischen Atomen zu verstehen. Vergleichen wir doch `mal die logischen Atome mit den Bausteinen eines Satzes, dem Subjekt und Prädikat. Wie Sätze zu Kapiteln eines Buches gefügt werden, setzen wir aus den Bausteinen die Häuser einer Stadt zusammen.``

,,So ähnlich könnte es gemeint sein``, sagte Hilde nachdenklich. ,,Die Korrespondenz zwischen Tatsachen und Aussagen wäre analog zur Beziehung zwischen Häusern und Sätzen denkbar. Die Sätze bildeten quasi den Plan zum Bau des Hauses. Wie ließe sich dieser Gedanke aber auf die Welt übertragen?`` grübelte Hilde weiter.

,,Die Welt nachgebaut aus logischen Atomen. Einige der Gebäude stimmen mit der Wirklichkeit überein; die meisten sind Phantasieprodukte. Diese Übereinstimmung könnte mit jener Korrespondenz gemeint sein``, ergänzte Sofie den Gedanken.

,,Dann wird auch Erfolg als Wahrheitskriterium plausibel. Wenn ich mit meinen Gebäuden in der Welt Erfolg habe, sind die Pläne wahr. Stürzen die Häuser ein, waren sie falsch. Nur nach wahren Naturgesetzen gebaute Maschinen funktionieren, erinnere ich einen Spruch unseres Physiklehrers``, sagte Hilde.

,,Aber mit Erfolg ist doch auch ein sportlicher oder wirtschaftlicher Aspekt verbunden``, gab Sofie zu bedenken. ,,Sind wir damit womöglich bei der schlechten Metaphysik angelangt?`` Hilde blätterte im Wörterbuch. ,,Aristoteles schrieb neben Büchern zur Logik und Physik noch weitere darüber hinaus gehende Werke, die er zur Metaphysik zusammenfaßte. Darin behandelt er Fragen des Seins und der Erkenntnis. Die entsprechenden Gebiete werden Ontologie und Epistemologie genannt. Zu deutsch: Seins- und Erkenntnislehre.``

,,Dann begünstigt schlechte Seins- und Erkenntnislehre politischen Totalitarismus``, ergänzte Sofie und fuhr fort: ,,Das Streben nach rigoroser Alleinherrschaft könnte auf den Nationalsozialismus in Deutschland zwischen 1933 und 1945 zugetroffen haben. Genaueres weiß ich aber nicht darüber ...``

,,Mein Vater sprach davon, daß religiöser Fundamentalismus oft Kriegsursache sei. Die schlechte Metaphysik der Religionen ist offenbar der Grund des Strebens nach Gewaltherrschaft``, erinnerte sich Hilde und sinnierte ihrem Vater folgend weiter: ,,Die Überwindung faschistischer Ideologien und abrahamitischer Religionen bleibt nach dem Fall des Sowjetkommunismus eine wichtige Aufgabe philosophischer Aufklärung ... ``

,,Bevor wir in die Politik abgleiten, sollten wir mit dem Studium Russells fortfahren``, unterbrach Sofie.

Bertrand Russell wurde am 18. Mai 1872 in Trellek (Wales) geboren. Er war der Sproß einer adligen Familie, die ihren Stammbaum auf Heinrich VIII (1509 - 47) zurückführte. Im Gegensatz zu vielen anderen Philosophen war Russell kein grüblerischer Eigenbrötler. Neben mehreren Liebschaften war er viermal verheiratet. Als kompromißloser Pazifist verlor er während des 1. Weltkrieges seine Professur am Trinity College in Cambridge und verbrachte ein halbes Jahr im Gefängnis. Bei einer Massenveranstaltung wurde er beinahe gelyncht. Nach der Geburt seines ersten Kindes 1921 hatte er Probleme bei der Wohnungsuche, da er moralisch unerwünscht war. Daraufhin kaufte er sich kurzerhand ein eigenes Haus. Später gründete er eine Schule, da keine der bestehenden Lehranstalten seinen Ansprüchen genügte. Ihm war insbesondere die christliche Intoleranz in der Erziehung zuwider. In den Jahren 1922 und `23 kandidierte er (natürlich erfolglos) für das Parlament.

,,In eine selbstverwaltete Schule wäre ich auch gerne gegangen ...``, meinte Hilde.

Ab 1944 war Russell wieder Professor in Cambridge. Nach dem Krieg engagierte er sich in der Friedensbewegung. Mit Einstein verfaßte er das Einstein-Russell-Manifest gegen das Wettrüsten. Seinem Projekt einer Gelehrtenkonferenz entsprang die Pugwash-Bewegung. Benannt nach dem kanadischen Ort ihrer ersten Zusammenkunft. Die Gelehrtenkonferernz entsprang der platonischen Staatsauffassung, nach der nur die weisesten Menschen politische Entscheidungsträger sein sollten. Ihr Einfluß auf die kruden Machtpolitiker blieb leider sehr gering. Anläßlich der Kubakrise initiierte er 1963 die Gründung der Bertrand Russell Peace Foundation. Sie unterstützte auch zahlreiche Initiativen zur Beendigung des Vietnamkrieges.

Trotz seiner zahlreichen Aktivitäten war Russell zeitlebens hauptsächlich als Schriftsteller tätig. Neben 70 Büchern zur Mathematik, Philosophie, Politik und Pädagogik verfaßte er unzählige Aufsätze und war weltweit auf Vortragsreisen unterwegs. Bevor er 1970 fast hundertjährig starb, konnte er auf ein erfülltes Leben zurückblicken:

Drei einfache, doch übermenschliche Leidenschaften haben mein Leben bestimmt: das Verlangen nach Liebe, der Drang nach Erkenntnis und ein unerträgliches Mitgefühl für die Leiden der Menschheit. Gleich heftigen Sturmwinden haben mich diese Leidenschaften bald hier-, bald dorthin geweht in einem launenhaften Zickzackkurs über ein Weltmeer von Qual hinweg bis zum letzten Rand der Verzweiflung.

Nach Liebe trachtete ich, einmal, weil sie Verzückung erzeugt, eine Verzückung so gewaltig, daß ich oft mein ganzes, mir noch bevorstehendes Leben hingegeben haben würde für ein paar Stunden dieses Überschwangs. Zum anderen habe ich nach Liebe getrachtet, weil sie von der Einsamkeit erlöst, jener entsetzlichen Einsamkeit, in der ein einzelnes erschauerndes Bewußtsein über den Saum der Welt hinabblickt in den kalten, leblosen, unauslotbaren Abgrund. Und letztens habe ich nach Liebe getrachtet, weil ich in der liebenden Vereinigung, in mystisch verkleinertem Abbild, die Vorahnung des Himmels erschaute, wie er in der Vorstellung der Heiligen und Dichter lebt. Danach habe ich gesucht und, wiewohl es zu schön erscheinen mag für ein Menschenleben: ich habe es - am Ende - gefunden. Mit gleicher Leidenschaft habe ich nach Erkenntnis gestrebt. Ich wollte das Herz der Menschen ergründen. Ich wollte begreifen, warum die Sterne scheinen. Ich habe die Kraft zu erfassen gesucht, durch die nach den Pythagoreern die Zahl den Strom des Seins beherrscht. Ein wenig davon, wenn auch nicht viel, ist mir gelungen.

Liebe und Erkenntnis, soweit sie erreichbar waren, führten empor in himmlische Höhen. Doch stets brachte mich das Mitleid wieder zur Erde zurück. Widerhall von Schmerzensgeschrei erfüllt mein Herz. Verhungernde Kinder, gefolterte Opfer von Unterdrückern, hilflose alte Menschen, ihren Kindern zur verhaßten Bürde geworden - die ganze Welt der Verlassenheit, der Armut, des Leids, all das macht ein hohnvolles Zerrbild aus dem, was Menschenleben eigentlich sein soll. Es verlangt mich danach, dem Übel zu steuern, allein ich vermag es nicht, und so leide auch ich.

So war mein Leben. Ich habe es lebenswert gefunden, und ich würde es mit Freuden noch einmal leben, wenn sich mir die Möglichkeit dazu böte.

,,Das muß ja ein interessanter Mensch gewesen sein``, staunte Sofie.

In Russells Einnerung verlief der erfüllteste Teil seiner Kindheit in Einsamkeit. Vor völliger Verzweiflung bewahrten ihn nur die Natur, die Bücher und die Mathematik. Seine Faszination für die Mathematik begann als ihn sein älterer Bruder mit elf Jahren in die Elemente der Euklidischen Geometrie einführte. Das wurde zu einem der größten Ereignisse seines Lebens. Die Schwierigkeiten bei der Annahme der Axiome ließen ihn fortan nicht mehr ruhen. Worin liegt das Geheimnis der mathematischen Wahrheit? Wie kann die Gewißheit der mathematischen Sätze mit dem Glauben an die Axiome vereinbart werden? Welcher Erkenntnis können wir überhaupt sicher sein?

Nach dem Studium der Mathematik und Philosophie in Cambridge begann er ab 1894 am Trinity College mit der Arbeit an einer logischen Begründung der Mathematik. Beflügelt durch die Erfolge Peanos und Hilberts bei der Axiomatisierung der Arithmetik und Geometrie machte er sich mit Whitehead daran, die Grundlagen der gesamten Mathematik nach logischen Prinzipien herzuleiten. Allein aus logischen Prinzipien sollten die mathematischen Wahrheiten gefolgert werden können! Diesem Projekt widmete er sich in den ersten zehn Jahren dieses Jahrhunderts. Einen Entwurf seines Projekts veröffentlichte er 1903 in den Prinzipien der Mathematik. Den Zusammenhang zwischen Sprache und Existenz untersuchte er 1905 in seiner Theorie der Beschreibung. Nicht viel später gelang ihm mit seiner Typentheorie die Lösung des Lügnerparadoxons und vieler weiterer Paradoxien der Sprache. Den Abschluß seiner logischen Forschungen bildeten die drei Bände der Principia Mathematica, die zwischen 1910 und 1913 erschienen. Nach dieser Zeit intellektueller Berauschtheit brachte der 1914 beginnende 1. Weltkrieg seinem Leben einen tiefen Einschnitt.

Als Kind hatte sich Bertrand vehement gegen die Annahme von Axiomen gestreubt. Nun überzeugte ihn Peano von der Fruchtbarkeit einer Axiomatisierung der Arithmetik. Was Russell an Peano am meisten beeindruckte, war die Klarheit seiner Argumente. In Diskussionen behielt er deshalb meist die Oberhand. Seine Axiome drücken die natürliche Zahlvorstellung aus, die dem allgemeinen Verständnis vom Zählen entspricht. Auf der Grundlage von fünf Axiomen konnte er alle Rechenregeln beweisen. Ausgehend von den natürlichen Zahlen können die ganzen-, rationalen-, reellen- und komplexen Zahlen jeweils durch Abstraktion gewonnen werden. Damit wird auch beweisbar, warum Minus Mal Minus Plus ergibt. Aber davon später. Um Euch nicht weiter im Unklaren zu lassen, will ich die Axiome Peanos hier wiedergeben:

Eins ist eine Zahl.
Der Nachfolger irgendeiner Zahl ist eine Zahl.
Eins ist nicht der Nachfolger irgendeiner Zahl.
Es gibt nicht zwei Zahlen mit demselben Nachfolger.
Jede Eigenschaft der Eins, die auch der Nachfolger jeder Zahl mit dieser Eigenschaft besitzt, kommt allen Zahlen zu.

Das fünfte Axiom wird Induktionsaxiom genannt. Mit Induktion wird der Schluß vom Einzelfall auf die Allgemeinheit bezeichnet. Im Gegensatz zu den anderen Axiomen ist es nicht unmittelbar einsehbar, oder? Die natürlichen Zahlen sind alle gleichartig und können durch fortgesetztes Hinzufügen eines Nachfolgers dargestellt werden. Das Induktionsaxiom überträgt das Bildungsgesetz der Zahlen auf die Eigenschaften der Zahlen. Bevor ich ein Beispiel gebe, will ich Euch eine logische Formulierung der Axiome zumuten.

Die Logik ist der auf das Schlußfolgern reduzierte Kern der Sprache. Wie in der Umgangssprache werden die logischen Ausdrücke nach Syntaxregeln aus einem Alphabet gebildet. Die Syntaxregeln werden auch Grammatik genannt. Gegeben seien:

Nominatoren:: Eigennamen und Kennzeichnungen: a, b, c, ...
Prädikatoren:: Eigenschaften und Relationen: A, B, C, ...
Junktoren:: Verbinder, wie und: 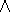, oder: 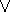, nicht: , wenn, dann: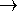
Quantoren:: der Allquantor für alle: , der Existenzquantor es gibt: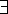
Gleichheit:: = bzw. ist identisch mit
Folgerung:: der logische Schluß:

Nominatorenvariablen werden durch kleine, Prädikatorenvariablen durch große Buchstaben bezeichnet. Durch Quantoren oder mit Bezug auf einen Gegenstandsbereich werden Variablen gebunden. Andernfalls kommen sie frei vor. Versucht Euch durch Vergleich mit den umgangssprachlich formulierten Axiomen an die logische Schreibweise zu gewöhnen. Im Gegensatz zu den Wörtern der Umgangssprache sind die logischen Symbole ganau definiert. Ich werde darauf zurückkommen. Die Gleichheit kennt Ihr schon aus dem Mathematik-Unterricht. Ein logischer Schluß überträgt die Wahrheit der Voraussetzungen (Prämissen) auf die Folgerung (Konklusion). Deshalb wird die Logik auch Theorie der Wahrheitsübertragung genannt.

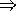
N(1)

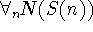
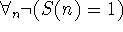
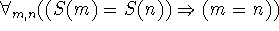
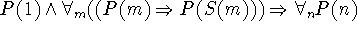
Seid Ihr mit der Zuordnung der Symbole zurechtgekommen? Das dritte Axiom läßt sich auch mit dem Existenzquantor schreiben: . Ist die logische Form des vierten Axioms mit der obigen Sprachform vereinbar: . Um die Rechenregeln der Arithmetik beweisen zu können, sind die Peano-Axiome um Definitionen (:=) der Addition (+) und Multiplikation (*) zu ergänzen:

D1: .
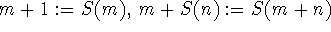D2: .

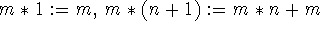Noch einfacher als die Logik mit Prädikatoren, die Prädikatenlogik, ist die Aussagenlogik. In ihr gibt es neben den Junktoren nur Aussagen. Das sind Sätze, die wahr oder falsch sein können. Sie werden nicht weiter in Nominatoren und Prädikatoren zergliedert. Ich greife die Unlogik Deines Schlusses von der achtsamen Rede auf, Sofie. Aus der Annahme, daß unachtsame Rede zu Widersprüchen führe folgt logisch, daß fehlende Widersprüche auf achtsame Rede schließen lassen. Im Schema: . Welche Sätze sind jeweils den Aussagenkonstanten a, w zugeordnet?

Aussagenschemata sind wahr für beliebige Aussagen. Ein Gegenbeispiel widerlegt sie. Das von Dir, Sofie, seinerzeit angenommene Schema ist nicht logisch wahr, da es Gegenbeispiele gibt: Bei Glatteis herrscht Unfallgefahr. Diese Voraussetzung liefe auf die Folgerung hinaus: Ohne Glatteis keine Unfallgefahr. Regennässe oder zu schnelles Fahren sind natürlich auch Unfallgefahren. Ihr seht, die Annahme dieses Trugschlusses hätte fatale Folgen! Nach obigem Schema kann lediglich gefolgert werden: Wenn keine Unfallgefahr, dann kein Glatteis.

Euch wird beim Nachvollziehen der Schemata nicht entgangen sein, daß ich stillschweigend die Gültigkeit der doppelten Verneinung benutzt habe: . Neben der Geltung des Satzes vom ausgeschlossenen Dritten ist die doppelte Verneinung das Kennzeichen der Klassischen Logik. Beide Annahmen gelten nicht in der Konstruktiven Logik.

,,Dann stören sich die Konstruktivisten also auch am Widerspruchsbeweis``, freute sich Hilde.

Bevor Ihr die Geduld verliert, ein Beispiel zum Induktionsaxiom! Wenn Ihr einen 10 DM-Schein (aus Deutschland) zur Hand haben solltet, schaut ihn Euch genau an. Er berichtet über den berühmten Mathematiker Carl Friedrich Gauß. Als Gauß noch klein war, wollte der Lehrer seine Klasse eine Zeitlang beschäftigen. Dazu stellte er ihnen die Aufgabe, die Zahlen von 1 bis 100 zu addieren. In der Hoffnung, damit ein wenig Ruhe zu haben, hatte sich der Pauker allerdings getäuscht. Schon nach kurzer Zeit meldete sich Carl und gab 5050 als richtige Lösung an. Der Lehrer war verblüfft und Ihr vielleicht auch? Carl hatte folgenden Trick benutzt:

Die vielen Additionsschritte hatte er auf nur eine Multiplikation und eine Addition zurückgeführt! Verwenden wir stellvertretend für die natürlichen Zahlen den Buchstaben i und als Abkürzung für die Summen das griechische Sigma . Damit können wir das Ergebnis folgendermaßen hinschreiben: . Wenn wir nun nachweisen wollen, ob die Gauß'sche Summationsformel nicht nur für 100, sondern für jede natürliche Zahl n gilt, haben wir das Induktionsaxiom anzuwenden. Daß sie für 1 gilt, ist klar. Durch Formelumwandlungen ist zu zeigen, daß die Summationsformel, wenn sie für n gilt, dann auch für n + 1 gilt:

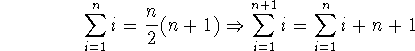
displaymath2477

Versucht das selbst nachzuvollziehen, bevor Ihr weiterlest. Was für endlich viele Zahlen direkt ausgerechnet werden kann, ist natürlich über jeden Zweifel erhaben. Wie sieht es aber mit der Übertragung des Induktionsaxioms auf unendlich viele Zahlen aus? Existiert überhaupt eine Summe über unendlich viele Zahlen? Mit der Abkürzung für unendlich läßt sich eine solche Summe zwar hinschreiben: . Ihre Bedeutung bleibt aber unklar.

,,Verstehst Du das?`` fragte Sofie gereizt und blickte Hilde an. Während sie ihre Aufmerksamkeit vom Text abwandten, vernahmen sie aus dem Garten Geräusche. Sie schauten aus dem Fenster und sahen drei merkwürdige Gestalten, die ihnen aber bekannt vorkamen. Die Mädchen traten vors Haus.

,,Wer seid ihr denn?`` wollte Hilde wissen.

,,Ich heiße Zeno``, sagte der älteste, ,,das sind Achilles und Theo Schildkröte. Sie sind hier, um einen Wettlauf über den Bootssteg zu veranstalten.``

,,Aber Achilles ist doch als schnellster Läufer bekannt. Eine Schildkröte wird gegen ihn keine Chance haben``, wunderte sich Sofie.

Zeno sah das anders: ,,Ich gebe Theo ein Stadion (192 m) Vorsprung. Obwohl Achilles zehn Mal schneller ist als die Schildkröte, wird er sie niemals einholen. Denn wenn Achilles den Vorsprung überwunden hat, kommt Theo um ein Zehntel dieser Strecke voran. Während Achilles den verbleibenden Vorsprung durcheilt, ist Theo wiederum ein Zehntel dieses Weges entfernt ... Das geht immer so weiter. Achilles wird die Schildkröte also niemals einholen können.``

Sofie und Hilde waren sprachlos. Was sollte man dagegen sagen? Die antiken Philosophen müssen es mit den Sophisten wahrlich schwer gehabt haben. Das Startsignal riß sie aus ihren Gedanken. Sie sahen die behäbigen Bewegungen Theos und verfolgten mit Spannung, wie der losrasende Achilles der Schildkröte rasch näher kam. Kurz bevor er sie einholte, war sie plötzlich verschwunden. Beide klatschten ins Wasser ...

,,Wenn der Steg länger gewesen wäre, hätte Achilles die Schildkröte überholt``, sagte Hilde und wollte sich an Zeno wenden. Der war aber nicht mehr aufzufinden. ,,Wir müßten uns ausrechnen können, wann Achilles Theo hätte einholen müssen``, kam sie ins Grübeln. Sie griff sich einen Stock und begann in den Sand zu schreiben. Sei v der Vorsprung, dann ist Theo dem Pelliden jeweils um voraus:

,,Kann die Summe denn endlich sein, obwohl sie sich über unendlich viele Zahlen erstreckt?`` wollte Sofie wissen.

,,Das sollten wir auszurechnen versuchen. Wir müßten dazu aber eine Summenformel finden``, sagte Hilde bekümmert. ,,Gauß hätte uns sicher weiterhelfen können ... Oder die Formelsammlung. Laß uns `reingehen und nachschlagen! Nach einigem Blätttern fanden sie eine geeignete Summenformel:

,,Wie man die Formel wohl beweist? Das Problem heben wir uns für später auf. Für wird immer kleiner. Im Grenzfall müßte es verschwinden``, legte Hilde los, so daß Sofie nur staunen konnte. Hilde schaltete den Computer ein und startete ein mathematisches Programmsystem. ,,Wenn wir den Wert von für den Vorsprung einsetzen, folgt:

Nach hätte Achilles Theo einholen müssen!`` begeisterte sich Hilde über ihr Ergebnis. Jetzt wissen wir, daß Zeno unrecht hatte und der Steg nicht viel länger als sein kann.``

,,Ich hab' nicht alles verstanden``, warf Sofie ein, ,,könnte die Rechnung nicht auch einfacher ausfallen? 1,11 ... ist doch bloß die Dezimalschreibweise der Summe: .``

,,Das gilt aber nur für diesen speziellen Fall. Ich suche allgemeine Lösungen für beliebigen Vorsprung v und einen n-Mal schnelleren Läufer.`` Unterdessen tippte Hilde folgende Zeile in den Rechner:

 evalf(sum(1/10^i,i=0..10)*192);

und erhielt als Egebnis 213.3333333. Wenn ich nun einem 2,5-Mal schnelleren Läufer einen Rückstand von

gebe, folgt mit

 evalf(sum(1/2.5^i,i=0..10)*100);

eine Strecke von 166.6596762.``

Sofie betrachtete fasziniert den Bildschirm: ,,Das Programm hätte ich auch gern in Mathe benutzt ...``

,,Vielleicht gibt es ja eine einfachere allgemeine Lösung ... ``, fuhr Hilde ungerührt fort: ,,Wir haben in Mathe zuletzt lineare Gleichungssysteme behandelt ... Zenos Bedingungen müßten sich damit eigentlich formulieren lassen. Wir setzen den Vorsprung gleich der Wegdifferenz zwischen Theo und Achilles: v = a - s. Zudem wissen wir, daß der Pellide n-Mal schneller ist als die Schildkröte, d.h. in gleicher Zeit n-Mal so weit kommt: a = n * s.`` Hilde tippte ein:

 solve({v=a-s,a=n*s},{a,s});

und erhielt die Lösungsmenge:

. Mit n = 10 und v = 192 kam heraus: s = 21,33, a = 213,33.

,,Sagenhaft!`` entfuhr es Sofie, ,,das habe ich verstanden. Schade, daß Du Zeno die Rechnungen nicht vorführen kannst.

,,Im Gegensatz zur unendlichen Summe natürlicher Zahlen, ist eine (unendliche) Summe über Brüche nicht immer bedeutungslos``, bemerkte Hilde nach einer Pause und schlug vor, im Text fortzufahren ...

Bedeutungslose Ausdrücke gibt es nicht nur in der Mathematik, viel häufiger kommen sie in der Umgangssprache vor. Denn mit vielen Worten oder Umschreibungen werden Dinge als existent vorausgesetzt, die es nicht gibt. Insbesondere die vergegenständlichende Rede im Deutschen wirkt fatal. Wer aus Adjektiven oder Verben Substantive bildet, läuft Gefahr über nichtexistente Dinge zu reden. Ein Beispiel: Die Röte der Sonne. Hat die Sonne Anteil an der Röte? Die Sonne scheint rötlich suggeriert nicht die Existenz einer Röte.

In seiner Theorie der Beschreibung analysiert Russell die mit der Sprache verbundenen Fallstricke beim Gebrauch von Namen, Kennzeichnungen und Abstrakta. Ein paar Beispiele:

Der gegenwärtige König von Frankreich hat eine große Nase.
Gott ist allmächtig.
Der Sinn des Lebens.
Jedes zweite Los gewinnt.
Sokrates war der Lehrer Platos und mußte den Schierlingsbecher trinken.

Im ersten Satz wird einem König eine große Nase zugesprochen, den es gar nicht gibt. Der Satz ist sprachlich nicht sinnlos, hat aber logisch keine Bedeutung. Es handelt sich um eine Pseudokennzeichnung. Im letzten Satz wird der Name Sokrates durch Kennzeichnungen präzisiert. Denn Namen können wir nur Dingen zusprechen, mit denen wir bekannt sind. Kennzeichnungen sollen Dinge in eindeutiger Weise beschreiben. Aus den verschiedenen Eigenschaften der Dinge muß geschlossen werden können, daß es sich um genau ein existierendes Ding handelt. In logischer Form: . D.h. es gibt einen durch Dokumente bezeutgen Menschen, der den Schierlingsbecher trank und Lehrer Platos war: Sokrates. Pseudokennzeichnungen sind leider weit verbreitet und tragen wesentlich zur sprachlichen Umweltverschmutzung bei.

Russells Theorie der Beschreibung ist nützlich, um Pseudokennzeichnungen zu entlarven und Scheinprobleme zu klären. Zu den Pseudokennzeichnungen gehören auch mathematische Terme, die enthalten. Oder Terme, in denen durch 0 dividiert wird. Anlaß vieler Scheinprobleme gibt die Verwendung von Abstrakta wie Sinn, Gott, Geist, der Wille, das Böse oder der Tod u.ä. Es soll Menschen geben, die an der Suche nach dem Sinn des Lebens verzweifeln. Sie sollten lieber an ihrer Existenzannahme des Sinns zweifeln. Schon die Existentialisten wiesen darauf hin: Es gibt keinen Lebenssinn! Nutze die Freiheit, ihn Dir zu schaffen! Es gibt auch keinen Gott oder Geist, ebenso weder das Böse oder den Tod. Was es gibt sind geistreiche, böse oder sterbende Menschen. Götter und Geister entstammen den Mythen. Aber nicht alle Abstrakta sind bedeutungslos. Im Abschlußkapitel werden wir ein Abstraktionsverfahren kennenlernen, daß sogar den Ansprüchen der Konstruktivisten genügt.

Beim Bau der Welt aus logischen Atomen, stellt die Beschreibungstheorie ein wichtiges Werkzeug im logischen Baukasten dar. Wenn Ihr darangeht, Texte nach Pseudokennzeichnungen zu durchforsten, werdet Ihr merken, wie leichtfertig voreilige Existenzannahmen gemacht werden. Erprobt Euren Scharfsinn an dem Satz: Jedes zweite Los gewinnt.

,,Den Satz hört man doch auf jedem Kirmis``, erinnerte sich Sofie.

,,Er suggeriert, daß die Hälfte der gekauften Lose Gewinne sind. Mehr noch, daß die Lose fortlaufend durchgemustert werden können und jedes zweite einen Gewinn verspricht``, entgegnete Hilde und empörte sich: ,,Nehmen wir an, jedes zweite Los werde als Gewinnlos gekennzeichnet, dann wird es viele Pseudokennzeichnungen geben. Denn eigentlich ist ja mit dem Spruch bloß gemeint, daß 50% der Lose im Eimer Gewinnlose sind. Liegen diese aber unten, wird es vorerst nur Verlierer geben!``

,,Und wenn die Nieten verbraucht sind, ist der Kirmis zu Ende. Welch ein Schwindel``, stimmte Sofie zu.