Extreme Physical Information

Naturvorgänge können durch Extremalprinzipien beschrieben werden, da sie in der Regel den Weg des geringsten Widerstandes gehen. Eine Kette ist so stark wie das schwächste Glied. So konnte schon Heron von Alexandria im 1. Jahrhundert das Reflexionsgesetz aus dem Prinzip des kürzesten Weges herleiten. Und das Brechungsgesetz läßt sich aus dem Prinzip der kürzesten Zeit berechnen. Euler und Lagrange verallgemeinerten die Prinzipien zum Prinzip der kleinsten Wirkung. Nach ihm verlaufen die Naturvorgänge so, daß der zeitliche Energieverlauf extremal, in der Regel minimal, wird. Aus diesem Prinzip folgt auch der Entropiesatz $dS \geq 0$.

Um nicht nur die Naturvorgänge, sondern auch die physikalische Theorienbildung aus einem Extremalprinzip verstehen zu können, hat sich der Physiker B. Roy Frieden die Definition von Information des Mathematikers Ronald Fisher zu nutze gemacht. Offensichtlich geht es beim physikalischen Experimentieren darum, ein Maximum an Information über die untersuchten Naturvorgänge zu gewinnen. Da aber jede Messung prinzipiell den Naturvorgang stört, den sie registrieren will, ist die Meßgröße grundsätzlich nur mehr oder minder genau schätzbar. Eine physikalische Messung gleicht somit einer Parameterschätzung, wie sie in der mathematischen Statistik untersucht wird. Nach einer von Cramer und Rao abgeleiteten Ungleichung besteht zwischen der Varianz e² und der Fisher-Information I folgender Zusammenhang:

$$e^2 I \geq 1\, \, bzw. \, \, I = 1/\sigma^2$$

Mit $\sigma^2$ als Varianz der Gauß'schen Normalverteilung folgt: Je größer die Varianz, d.h. je stärker die Meßgroße gestört ist, desto kleiner ist die Information der Messung. Ein intuitiv einleuchtender Zusammenhang.

Sei q(x) die Wahrscheinlichkeits-Amplitude für die Störung x bei einer Einzelmessung, dann folgt für die Fisher-Information:

$$I = 4 \int dx \left({dq \over dx}\right)^2$$

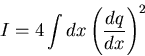
Für die Änderung dI der Information gilt: $dI \leq 0$. Im Gegensatz zur Entropie hat die Information die Tendenz abzunehmen. Wie in der Thermodynamik läßt sich auch hier eine Temperatur definieren:

$${1 \over T} = -k {\partial I \over \partial E}$$

Ziel einer Messung ist es, die Information über das physikalische System zu maximieren. Wird die im System gebundene Information mit J bezeichnet, geht es um eine Informationsübertragung von J nach I. Extreme Physical Information (EPI) meint also folgendes:

$$K = I - J = extrem. \, \, bzw. \, \, I - \kappa J = 0$$

Mit K wird die physikalische Information bezeichnet und $\kappa$ meint die Effizienz der Informationsübertragung. Die Anwendbarkeit von EPI setzt offensichtlich die Existenz von Informationsdichten $i_n,\, j_n$ voraus, wobei gilt:

$$i_n = 4 \vec{\nabla }q_n \vec{\nabla }q_n$$

Damit wird $I = \int d\vec{x} \sum i_n(\vec{x})$. Eine entsprechende Gleichung folgt für J. Der Meßprozeß erzeugt ein Wahrscheinlichkeitsgesetz der physikalischen Theorie, nach dem die Daten gesammelt werden bzw. die Messung abläuft. Je nach Wahl der Invarianzforderungen, die an die Informationsübertragung zu stellen sind, kann eine Optimierung der physikalischen Information erreicht werden. Dabei zeigt sich insbesondere, daß die Quantenmechanik im Vergleich mit der klassischen Mechanik die Informationsübertragung maximiert.

Der Gedankengang Friedens läßt sich wie folgt zusammenfassen. Eine Messung machen heißt, in quantitativer Weise eine Frage stellen. Die Meßdaten werden durch physische Vorgänge verursacht. Eine Messung erzeugt die Wahrscheinlichkeitsverteilung, aus der die Meßdaten zu extrahieren sind. Existiert ein physikalisch interpretierter, geeignet invarianter Transformationsraum, dann EPI! EPI optimiert also einen physischen Prozeß und ermöglicht die Formulierung physikalischer Verlaufsgesetze, die sich wiederum experimentell bewähren.