Gödels Unvollständigkeitssatz

GEB

Zusammenfassung:

Eine poetische Übersicht und grundsätzliche Erläuterungen zum Gödel'schen Unvollständigkeitsbeweis.

Das Verständnis des Gödel'schen Satzes wird erleichtert, wenn man von der Epimenides-Paradoxie in der Quine'schen Form ausgeht: Ergibt eine Unwahrheit, wenn sein Zitat vorangeht ergibt eine Unwahrheit, wenn sein Zitat vorangeht. Einem Satz das Zitat seiner selbst voranzustellen, wird auch quinieren genannt. Das umgangssprachliche Zitat einer Unwahrheit ihrerselbst hat Gödel in einen Satz der Zahlentheorie übertragen. Sein Beweis läßt sich in einige wesentliche Schritte unterteilen:

Zahlenkalkül

Als Zahlenkalkül werde die mit den Mitteln der Prädikatenlogik formalisierte Arithmetik bezeichnet (vgl. Peano-Axiome).

Gödelisierung

Allen Ausdrücken des Zahlenkalküls werden (umkehrbar eindeutig) Zahlen zugeordnet. D.h. jedem Satz des Kalküls entspricht genau eine Satz-Zahl, die Gödelnummer. Auf die Umgangssprache bezogen, entspricht die Gödelnummer dem Zitat eines Satzfragments.

Beweispaar

Die Eigenschaft, ein Satz des Kalküls zu sein, wird (innerhalb des Kalküls) ausgedrückt durch Angabe eines ableitbaren Beweispaares: B(a, a'). In ihm steht a für die Gödelnummer der Ableitung und a' für die Gödelnummer des letzten Schrittes der Ableitung; also des Satzes selbst. a' ist eine Satz-Zahl des Zahlenkalküls wird ausgedrückt durch: 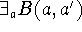. D.h. es gibt eine Ableitung mit der Gödelnummer a, deren letzter Schritt die Gödelnummer a' hat. Es ist wichtig, zu beachten, daß ein Beweispaar keinen (ableitbaren) Satz repräsentiert. Ein Beweispaar erlaubt es lediglich, mit den Mitteln des Kalküls über die Ableitbarkeit eines Satzes zu sprechen.

Substitution

Es werden alle freien Variablen eines Satzes durch eine Zahl ersetzt. Dabei ist die Beziehung zwischen

• der ursprünglichen Gödelnummer a,
• der Zahl a', die eingesetzt wird,
• und der sich daraus ergebenden Gödelnummer a''

ableitbar. Diese Substitutions-Operation werde abgekürzt durch: E(a, a', a''). Umgangssprachlich wird einem Prädikat ein Subjekt vorangestellt.

Quinierung

Um einen Satz des Kalküls herzustellen, der über sich selbst spricht, ist eine Substitution mit der Gödelnummer des Satzes selbst vorzunehmen: E(a', a', a''). Diese selbstbezügliche Substitution folgt der Formulierung, die Quine der Epimenides-Paradoxie gab. Sie werde abgekürzt durch: Q(a'', a'). D.h. a' ist die Quinierung von a'' (in E war es umgekehrt). Wie der Vergleich mit der allgemeinen Substitution zeigt, hat a'' bei der Quinierung eine doppelte Bedeutung! Umgangssprachlich stellt die Quinierung einem Prädikat das Zitat seiner selbst voran.

Um einen Satz zu quinieren, in dem die Quinierung erwähnt wird, ist die Quinierung mit dem entsprechenden Beweispaar zu verbinden:

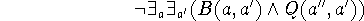
Dieser Satz wird Gödels Onkel genannt. Umgangssprachlich bedeutet er: ergibt eine Unwahrheit, wenn quiniert.

Gödels Satz

Sei u die Gödelnummer von Gödels Onkel. Dann ergibt seine Quinierung Gödels Satz G:

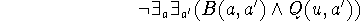
G's Gödelnummer a' ist die Quinierung von u. G sagt aus, daß es kein a gibt, das mit der Quinierung von u ein Beweispaar bildet. D.h. G sagt von sich selbst aus, kein Satz des Zahlenkalküls zu sein! Unter der Voraussetzung, daß der Zahlenkalkül widerspruchsfrei ist, kann G nur wahr sein. D.h. es gibt einen wahren Satz des Zahlenkalküls, der von sich selbst behauptet, daß er nicht ableitbar ist!! Umgangssprachlich formuliert lautet Gödels Ergebnis: ergibt eine Unwahrheit, wenn quiniert ergibt eine Unwahrheit, wenn quiniert. Dieser Satz entspricht der ursprünglichen Quine'schen Version der Epimenides-Paradoxie.